論理積【AND演算】logical conjunction/logical product

概要

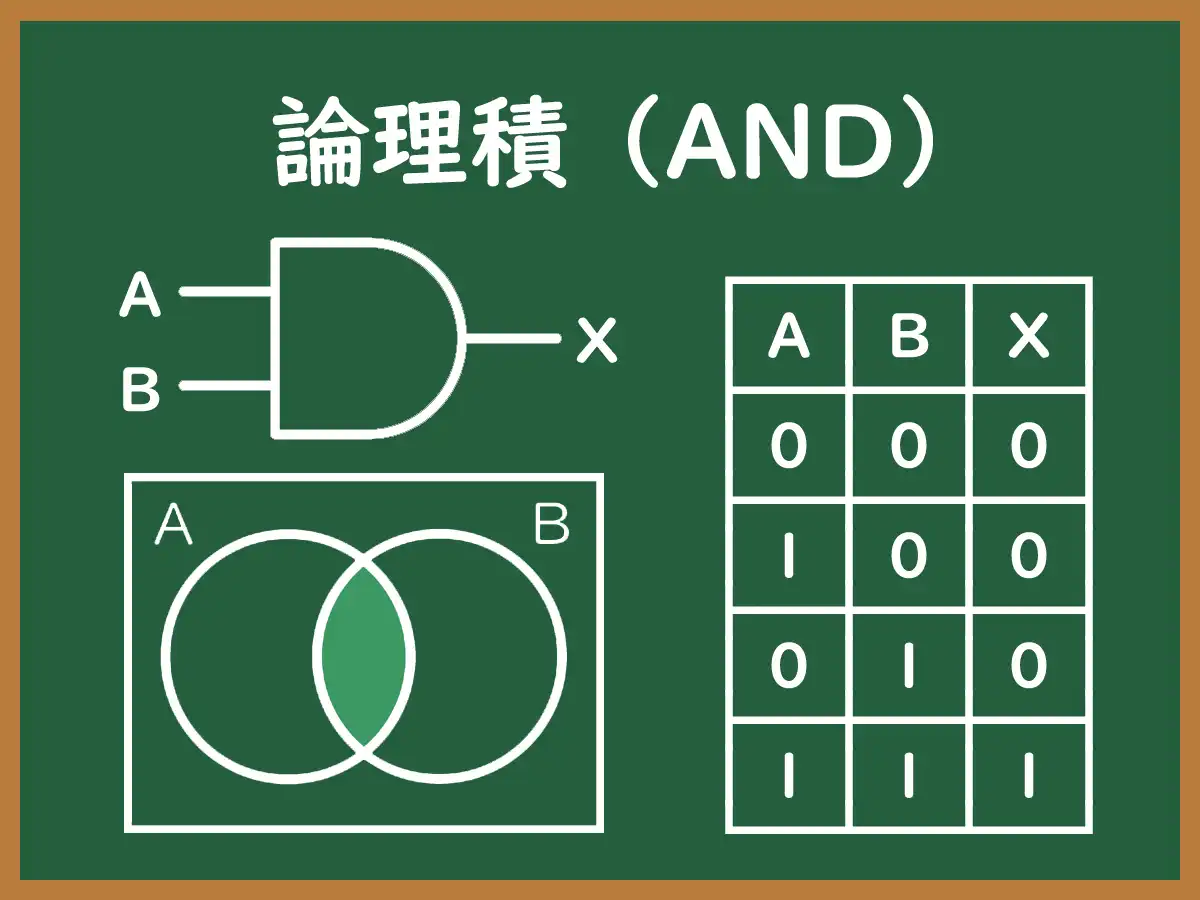
論理学では記号「∧」を用いて「P∧Q」のように表記し、電子工学（論理回路）では記号「⋅」を用いて「P⋅Q」のように表す。論理積演算を行う論理回路を「論理積演算回路」「AND演算回路」「ANDゲート」などと呼ぶ。

多くのプログラミング言語でもビットごとの論理積演算を行う演算子が用意されており、キーワード「and」を用いて「P and Q」と書くものや、C言語に倣って「&」（アンパサンド）記号を用いて「P&Q」と表記する言語が多い。また、ビット演算と区別して条件式などで用いる真偽値（真理値）の論理積演算を定義している言語では、「and」キーワードや「&&」などの記号が用いられることが多い。

三入力以上の場合は、まず二つを選んで論理積を取り、その結果と残りの一つを選んで論理積を取り、という手順を繰り返すことで結果を得ることができ、すべての入力が1のときのみ出力が1となり、いずれかの入力が0の場合には0となる。

論理積は論理和（OR演算）と論理否定（NOT演算）を組み合わせて P∧Q ⇔ ¬（¬P∨¬Q） と表すことができる。逆に、論理和は論理積と論理否定を組み合わせて P∨Q ⇔ ¬（¬P∧¬Q） と表すことができる。これをド・モルガンの法則という。