ベン図【Venn diagram】

概要

ベン図（Venn diagram）とは、集合間の関係を表す図法の一つ。集合の範囲を円などの図形で表し、図形の重なりによって共通部分を表現する。19世紀の終わり頃、イギリスの数学者ジョン・ベン(John Venn)によって考案された。

まず大きな長方形などで描画範囲を設定し、これをすべての要素が含まれる全体集合とする（この領域は設定しない場合もある）。個々の集合は円や楕円などの図形で表される。集合間に共通の要素がある場合、図形の一部を重ねて表現する。

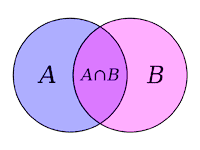
集合Aを円で表すとき、Aの外側はAの補集合（A、A^c）を表す。集合Bも円で表すと、両者の重なった領域が共通部分（A∩B）、重なりも含め両者を合わせた領域が和集合（A∪B）を表す。BがAに完全に含まれる場合、BはAの部分集合（A⊃B）となる。

3つ以上の集合の関係も図示できるが、4つ以上は重なり方の組み合わせを漏らさず図示するのが難しくなるため、あまり用いられない。説明のために集合ごとに色や模様で塗り分けたり、現在着目している領域のみを着色することが多い。黒で塗られた領域は元が存在しないことを表すため、塗り分けで黒を用いることは控える。

集合演算の結果を視覚的に分かりやすく表すことができるため、これを論理演算の図示に応用することもある。変数を円に対応付け、円の内部を真（true）または1、外側を偽（false）または0に対応付ける。例えば、2変数PとQの場合、円Pの外側がPの論理否定（not P/￢P）、円の重なりが論理積（P and Q/P∧Q）、両円を合わせた領域が論理和（P or Q/P∨Q）に対応する。

(2022.4.28更新)