平均絶対誤差 【Mean Absolute Error】

概要

平均絶対誤差（Mean Absolute Error）とは、実際の値と何らかのモデルに基づく予測値があるとき、両者の差の絶対値を平均した値。予測モデルの評価に用いられる。

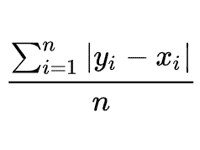
ある事象について実際に測定、観測などで確かめた値と、それぞれの値が得られた条件に基づいて予測関数などから導き出された予測値があるとき、両者の差（予測値の真値からの誤差）を求め、その絶対値を平均することで求められる。

予測値が真値に近ければ近いほど平均絶対誤差は小さくなり、逆に真値からのズレが大きくなればなるほど平均絶対誤差も大きくなる。すべての真値を言い当てることができる完璧な予測モデルの場合には平均絶対誤差の値は0となる。

誤差の評価法として最も単純な手法の一つで、計算が容易で直感的に理解しやすく、二乗誤差などに比べ外れ値の影響を受けにくいなどの特徴がある。真値や予測値と次元が同じであるため損失関数として用いることもある。

予測モデルの誤差評価法としては他に、誤差の真値に対する割合（パーセンテージ）で表す「平均絶対パーセント誤差」（MAPE：Mean Absolute Percentage Error）や、誤差の二乗平均を取る「平均二乗誤差」（MSE：Mean Squared Error）などがある。

(2023.11.2更新)

他の辞典による解説 （外部サイト）

この記事の著者 ： (株)インセプト IT用語辞典 e-Words 編集部
1997年8月より「IT用語辞典 e-Words」を執筆・編集しています。累計公開記事数は1万ページ以上、累計サイト訪問者数は1億人以上です。学術論文や官公庁の資料などへも多数の記事が引用・参照されています。
ホーム画面への追加方法
1.ブラウザの 共有ボタンのアイコン 共有ボタンをタップ
2.メニューの「ホーム画面に追加」をタップ
閉じる