単回帰分析【simple regression】

概要

単回帰分析（simple regression）とは、2つのデータ系列の間に原因と結果という関係があると考えられるとき、原因のデータから結果のデータを導き出す規則性を明らかにすること。

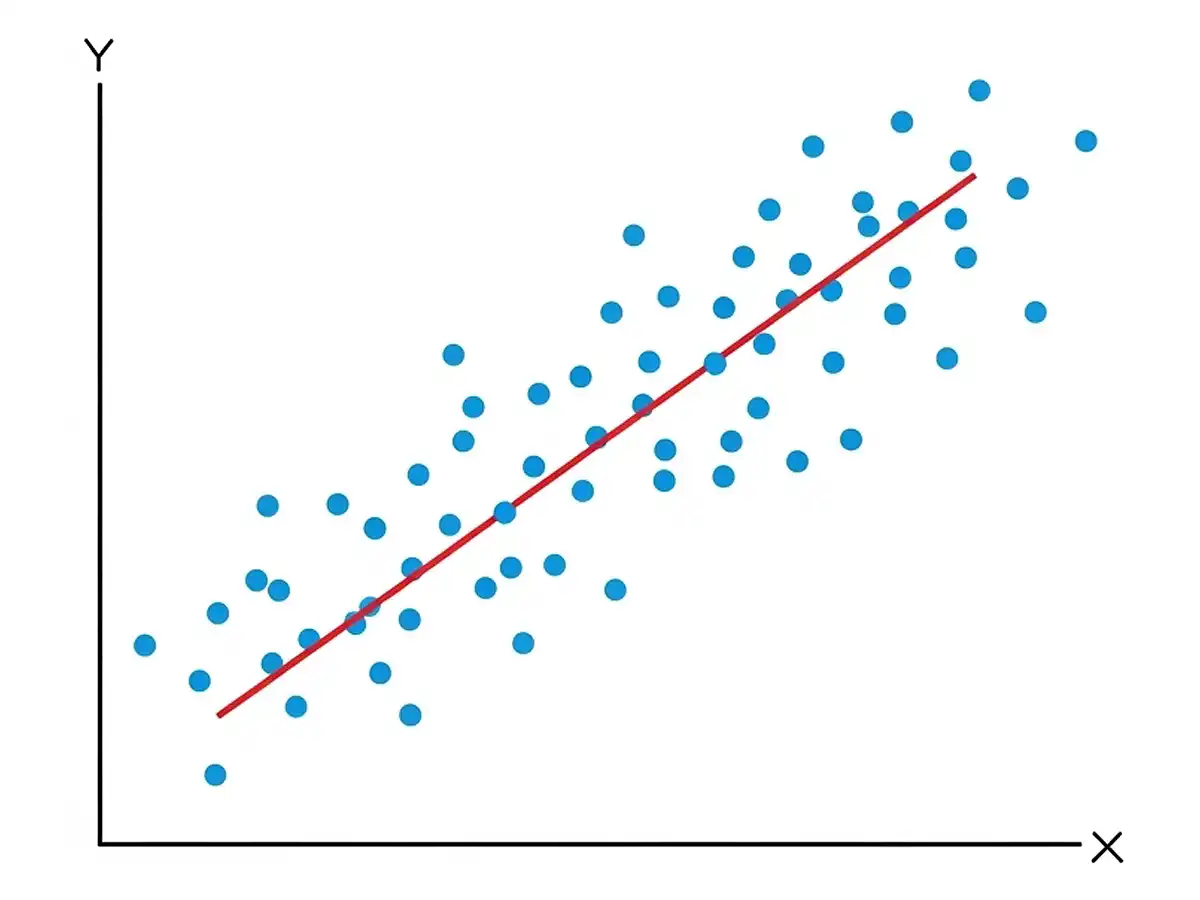
調査や測定などで2つの変数の関係について得られたデータを元に、結果と考えられる変数（目的変数）が原因と考えられる変数（説明変数）からどのような影響を受けているかを関数（数式）の形で明らかにする。なお、説明変数が複数ある場合の回帰分析は「重回帰分析」という。

例えば、ある飲食店のビールの売上（y）とその日の最高気温（x）についての記録を単回帰分析したところ、定数a、bを用いて $y = ax + b$ という1次関数の形で表されたとする。この関係が分かれば、天気予報を元に仕入れ量を調整することができる。

この例では説明変数と目的変数が1次関数で表される直線的な比例関係にあることを仮定しており、これを「線形回帰」あるいは「直線回帰」という。物事の関係性は比例関係で表されるとは限らず、 $x^{2}$ のような高次の項を含む多項式、指数関数、対数関数、三角関数などが含まれる場合がある。このような正比例以外の関係を含む回帰を総称して「非線形回帰」という。

統計値などから単回帰分析を行う場合、各標本は誤差を含んで一定の範囲にばらついているため、数値計算を繰り返して関数のパラメータ（係数）を推定する。代表的な手法として「最小二乗法」がよく知られ、回帰式から得られる値と各標本の実際の値の誤差を二乗して足し合わせた値が最小になるよう係数を決定する。

(2024.5.26更新)