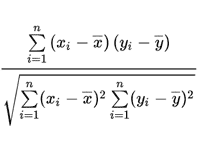回帰分析【regression analysis】

概要

回帰分析（regression analysis）とは、何かの結果を表す数値があるとき、原因と考えられる数値がどのような形で影響を与えているのか規則性を明らかにすること。因果関係の推定や事象の予測、シミュレーションなどのためによく行われる。

調査などで得られた様々な数値の組み合わせのうち、着目している数値（従属変数）が、他の数値（説明変数）からどのように影響を受けているかを関数の形で明らかにする。説明変数が一つの場合を「単回帰分析」、複数の場合を「重回帰分析」という。

例えば、ある飲食店のビールの売上（y）とその日の最高気温（x）についての記録を単回帰分析したところ、y=ax+c という1次関数の形で表されたとする。この関係が分かれば、天気予報を元に仕入れ量を調整することができる。降水量（z）との関係も合わせて重回帰分析することで、y=ax+bz+c という関係が明らかになれば、より精度の高い予測が可能となる。

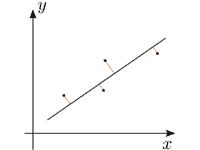
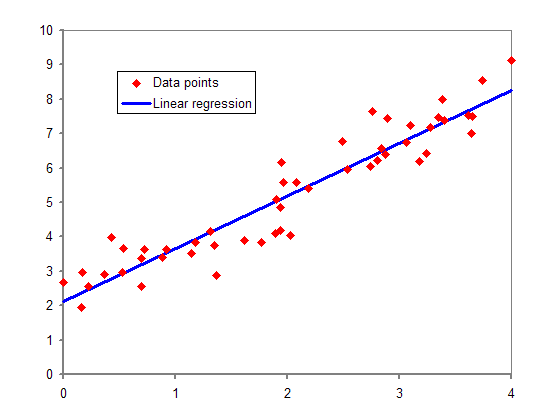
この例では説明変数と従属変数が直線的な比例関係で表されることを仮定しており、これを「線形回帰」あるいは「直線回帰」という。物事の関係性は単純な比例関係で表されるとは限らず、x² のような高次の項を含む多項式、指数関数、対数関数、三角関数などが含まれる場合がある。これを「非線形回帰」という。

統計値などから回帰分析を行う場合、各標本は誤差を含んで一定の範囲にばらついているため、数値計算を繰り返して関数のパラメータ（係数）を推定する。代表的な手法として「最小二乗法」がよく知られ、回帰式から得られる値と各標本の実際の値の誤差を二乗して足し合わせた値が最小になるよう係数を決定する。

(2023.9.10更新)