対数 【logarithm】 log

概要

対数（logarithm）とは、ある数を何乗すると指定の数になるかを表す指数のこと。ある数bをa乗するとpになる($b^a=p$)とき、指数aのことを「bを底ていとするpの対数」という。

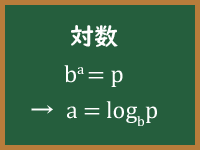
同じ数を何度も掛ける冪乗の計算で、掛ける回数に相当する数を「指数」（exponent）というが、掛ける数と掛けた結果の数が分かっているときに、指数がいくつになるかを表したものが対数である。

例えば、2の3乗は $2\times 2\times 2$ で8（$2^3=8$）となるが、2と8が分かっているとき、2を8にするための指数3を「2を底とする8の対数」と表現し、「${\log }_{2}8=3$」のように表記する。8のことを「真数しんすう」と呼ぶことがある。底は1以外の正の値で、真数は正の数である必要がある。冪乗計算では $b^x{b}^y=b^{x+y}$ となるため、対数計算でも ${\log }_b\mathrm{XY}={\log }_{b}X+{\log }_{b}Y$ が成り立つ。

数学では底を10とする「常用対数」（common logarithm）を用いることが多く、底を省略して「$\log x$」のように表記することが多い。また、ネイピア数 $e$ を底とする対数を「自然対数」（natural logarithm）と呼び、「$\ln x$」のように表記する。コンピュータ科学では2進数を多用する関係で2を底とした対数（binary logarithm）を用いることが多く、底を省略したら2とみなす慣習がある。