平均二乗誤差 【MSE】 Mean Squared Error

概要

平均二乗誤差（MSE）とは、実際の値と何らかのモデルに基づく予測値があるとき、両者の差を二乗して平均した値。予測モデルの評価に用いられる。

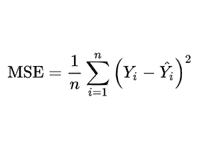
ある事象について実際に測定、観測などで確かめた値と、それぞれの値が得られた条件に基づいて予測関数などから導き出された予測値があるとき、両者の差（予測値の真値からの誤差）を二乗して足し合わせ、標本の数で割って平均を求めた値である。

予測モデルから得られた値が真の値に近ければ近いほど平均二乗誤差は小さくなり、逆に真値からのズレが大きくなればなるほど平均二乗誤差も大きくなるという関係にある。すべての真値を言い当てることができる完璧な予測モデルの場合には平均二乗誤差の値は0となる。

平均二乗誤差は二乗した値の平均であるため真値や予測値とは次元が異なり、同じ尺度で比較できない。このため、平均二乗誤差の平方根（ルート）を取って同じ次元に戻す操作を行った値で評価することもある。これを「平均二乗平方根誤差」（RMSE：Root Mean Squared Error）という。

この記事の著者 ： (株)インセプト IT用語辞典 e-Words 編集部
1997年8月より「IT用語辞典 e-Words」を執筆・編集しています。累計公開記事数は1万ページ以上、累計サイト訪問者数は1億人以上です。学術論文や官公庁の資料などへも多数の記事が引用・参照されています。