読み方：かいきちょくせん

回帰直線【regression line】

概要

回帰直線とは、2つのデータ系列を描画した散布図で、分布の傾向に最もよく当てはまるように引いた直線のこと。2つの系列の関係を一次関数として近似している。

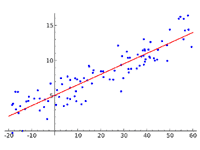
測定値などの分布に基づいて、2つの変数の関係を $y = ax + b$ という一次関数で近似することを線形単回帰という。 $x$ を説明変数、 $y$ を目的変数と呼び、 $x$ の値から未知の $y$ を予測・推測できるようになる。

2つの変数の関係について、横軸を説明変数、縦軸を目的変数とする散布図で表したときに、分布の様子を直線で近似したものを回帰直線という。回帰分析で求めた一次関数（回帰式）をグラフ上に描画したものである。先の方程式の $a$ は直線の傾きを、 $b$ はy切片を表している。

回帰直線は実際のデータを表す各点との距離がなるべく小さくなることが望ましい。この条件を満たすため、一般的には「最小二乗法」という計算法で係数 $a$ と $b$ の値を決定する。説明変数 $x_{i}$ において、実測された目的変数は $y_{i}$ 、回帰式から求めた予測値は $a x_{i} + b$ となる。

両者の差である $y_{i} - a x_{i} - b$ を2乗し、各点について合計したものを残差平方和という。これが最小になるときの $a$ および $b$ を算出すると、 $x$ と $y$ の平均 $\bar{x}$ と $\bar{y}$ 、標準偏差 $S_{x}$ と $S_{y}$ 、相関係数 $r$ を用いて、 $b = r \frac{S_{y}}{S_{x}}$ 、 $a = \bar{y} - b \bar{x}$ として表すことができる。