標準偏差 【SD】 Standard Deviation

概要

標準偏差（SD）とは、統計における指標の一つで、データ群のばらつき具合を表す値。この値が小さいほど平均付近にデータが集まっていることを表し、大きければ平均から外れたデータがたくさんあることを表している。

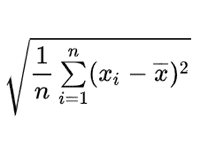
標準偏差は分散の正の平方根で、データが平均値から平均でどのくらい離れているかを表している。算出方法は、各値と平均値の差を二乗した値の和を求め、これをデータの数で割った平均のルートを取る（二乗平均平方根）。

例えば、{10,20,30} という3つの標本の標準偏差は、平均値20を用いて √[{（10-20）2+（20-20）2+（30-20）2}/3] と表され、約8.16となる。{0,20,40} ならば約16.33となり、すべて平均値に等しい {20,20,20} ならば標準偏差は0となる。

分散も散らばり具合を表しているが、元の値と平均の差の二乗の平均であるため、元の値とは次元が異なる。標準偏差はその平方根を取っているため、元の値と同じ次元となり、値自体の大きさと散らばり具合の大きさを同じ尺度で比較することができる。日本では学力試験のいわゆる偏差値を算出するのに用いられている。

(2023.9.22更新)

他の辞典による解説 （外部サイト）

この記事の著者 ： (株)インセプト IT用語辞典 e-Words 編集部
1997年8月より「IT用語辞典 e-Words」を執筆・編集しています。累計公開記事数は1万ページ以上、累計サイト訪問者数は1億人以上です。学術論文や官公庁の資料などへも多数の記事が引用・参照されています。
ホーム画面への追加方法
1.ブラウザの 共有ボタンのアイコン 共有ボタンをタップ
2.メニューの「ホーム画面に追加」をタップ
閉じる