正規分布【normal distribution】ガウス分布 / Gaussian distribution

概要

正規分布（normal distribution）とは、統計学で用いられる確率分布の一つで、平均付近に分布が集中し、平均から乖離するに連れ指数的に頻度が減少していくような分布のこと。自然現象や社会現象の多くがこの分布に従うことが知られており、確率・統計を扱う上で最も重要かつ基本的な分布である。

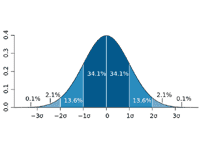
平均値、中央値、最頻値が同一の左右対称な分布で、横軸が値、縦軸が確率となるグラフに図示すると釣り鐘のように平均付近が大きく膨らんだ形状（ベルカーブという）となる。誤差や個体差など自然に生まれる値のばらつきの多くは正規分布に従って分布する。

ある値xが出現する確率を表す確率密度関数は、平均値μと標準偏差σを用いて 1/√（2πσ）×e^{-（x-μ）²/2σ²} という式で表される。同じ正規分布でも平均値が異なれば確率が最大になる位置が異なり、標準偏差が異なれば平均への偏り具合が異なる。標本値を線形変換し、平均が0、標準偏差が1になるように調整した分布を「標準正規分布」という。

正規分布の重要な性質として、平均μや標準偏差σの違いによらず、σの倍数で表される区間に値が含まれる確率は常に一定であるというものがある。例えば、平均から標準偏差だけ離れた範囲（μ-σからμ+σまで）に値が含まれる確率は約68.27%、μ±2σの範囲なら約95.45%、μ±3σの範囲なら約99.73%となる。

(2023.9.25更新)