楕円曲線暗号【ECC】 Elliptic Curve Cryptography

概要

楕円曲線暗号（ECC）とは、楕円曲線上の離散対数問題と呼ばれる数学上の問題を安全性の根拠とする暗号。1985年に暗号学者のビクター・ミラー(Victor Miller)氏とニール・コブリッツ(Neal Koblitz)氏が独立にほぼ同時に考案した。楕円曲線DSA(ECDSA)や楕円曲線Diffie Hellman鍵交換(ECDH)などに応用されている。

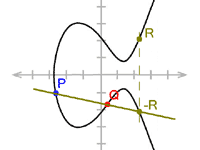
楕円曲線とは y² = x³ + ax + b という形で表される曲線で、この曲線上の二点の座標の関係について特殊な加算法を定義する。ある点Gについて自身を加算することにより「2倍」を求めることができるが、これを繰り返すことで任意のn倍（nG）を求めることができる。また、加算を続けていくとp回後に再びGに戻ってくることが知られており、どのような加算の結果もp個の点のうちのいずれかを指すことになる。

Gをn倍すると点Xに到達する場合に、nとGからXを求めるのは容易な一方、XとGからnを求める（XはGを何倍したものかを割り出す）ことは困難で、効率よく計算する方法は発見されていない。これを楕円曲線上の離散対数問題（ECDLP：Elliptic Curve Discrete Logarithm Problem）と呼び、nを元に秘密鍵を、GとXを元に公開鍵を生成することで、公開鍵が知られても秘密鍵を割り出すことが困難な公開鍵暗号を構築することができる。

ただし、曲線のパラメータや計算を開始する点Gの選び方によってはnが容易に計算できてしまう場合があるため、実用上はpが十分大きな素数となるよう各値を設定する必要がある。

公開鍵暗号としては他に、巨大な素数の積の素因数分解の困難さを基礎とするRSA暗号が広く知られているが、楕円曲線暗号はより短い暗号鍵で同程度の暗号強度が得られ、暗号化や復号に伴う計算回数も少ないことから、ICカードなど処理能力の限られた機器で早くから実用化されているほか、これまでRSAが用いられてきた用途でも導入や置き換えが進みつつある。

(2018.7.9更新)