基本情報技術者(科目A)過去問集 - 離散数学
令和7年6月修了試験 問1
16進小数 0.C を10進小数に変換したものはどれか。
| ア | 0.12 |
|---|---|
| イ | 0.55 |
| ウ | 0.75 |
| エ | 0.84 |
令和7年1月修了試験 問1
| ア | 0~255 |
|---|---|
| イ | -127~127 |
| ウ | -127~128 |
| エ | -128~127 |
令和6年12月修了試験 問1
数多くの数値の加算を行う場合,絶対値の小さなものから順番に計算するとよい。これは,どの誤差を抑制する方法を述べたものか。
| ア | アンダフロー |
|---|---|
| イ | 打切り誤差 |
| ウ | けた落ち |
| エ | 情報落ち |
令和6年12月修了試験 問2
0~9の数字と空白文字を組み合わせて長さ3の文字列を作る。先頭1文字には数字を使えるが,空白文字は使えない。2文字目以降には空白文字も使えるが,空白文字の後に数字を並べることは許されない。何通りの文字列を作ることができるか。ここで,同じ数字の繰返し使用を許すものとする。
| ア | 1,110 |
|---|---|
| イ | 1,111 |
| ウ | 1,210 |
| エ | 1,331 |
令和6年7月修了試験 問1
浮動小数点演算において,絶対値の大きな数と絶対値の小さな数の加減算を行ったとき,絶対値の小さな数の有効桁の一部又は全部が結果に反映されないことを何というか。
| ア | 打切り誤差 |
|---|---|
| イ | 桁落ち |
| ウ | 情報落ち |
| エ | 絶対誤差 |
令和6年6月修了試験 問1
数値を2進数で格納するレジスタがある。このレジスタに正の整数xを設定した後,“レジスタの値を2ビット左にシフトして,xを加える” 操作を行うと,レジスタの値はxの何倍になるか。ここで,あふれ(オーバフロー)は,発生しないものとする。
| ア | 3 |
|---|---|
| イ | 4 |
| ウ | 5 |
| エ | 6 |
令和6年公開問題 問1
X 及び Y はそれぞれ0又は1の値をとる変数である。X□Y をXとYの論理演算としたとき,次の真理値表が得られた。X□Y の真理値表はどれか。
| X | Y | X AND (X□Y) | X OR (X□Y) |
| 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 |
| ア |
| |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| イ |
| |||||||||||||||
| ウ |
| |||||||||||||||
| エ |
|
令和5年7月修了試験 問1
| ア | A - B |
|---|---|
| イ | (A∪B)-(A∩B) |
| ウ | (S - A)∪(S - B) |
| エ | S -(A∩B) |
令和5年1月修了試験 問1
| ア | |
|---|---|
| イ | |
| ウ | |
| エ |
令和5年1月修了試験 問2
P,Q,Rはいずれも命題である。命題Pの真理値は真であり,命題(not P)or Q 及び命題(not Q)or R のいずれの真理値も真であることが分かっている。Q,Rの真理値はどれか。ここで,X or Y はXとYの論理和,not X はXの否定を表す。
| Q | R | |
| ア | 偽 | 偽 |
| イ | 偽 | 真 |
| ウ | 真 | 偽 |
| エ | 真 | 真 |
令和4年12月修了試験 問1
桁落ちの説明として,適切なものはどれか。
| ア | 値がほぼ等しい浮動小数点数同士の減算において,有効桁数が大幅に減ってしまうことである。 |
|---|---|
| イ | 演算結果が,扱える数値の最大値を超えることによって生じるエラーのことである。 |
| ウ | 浮動小数点数の演算結果について,最小の桁よりも小さい部分の四捨五入,切上げ又は切捨てを行うことによって生じる誤差のことである。 |
| エ | 浮動小数点数の加算において,一方の数値の下位の桁が結果に反映されないことである。 |
令和4年7月修了試験 問1
| ア | (10.101)2×2-16-(1.001)2×2-15 |
|---|---|
| イ | (10.101)2×216-(1.001)2×216 |
| ウ | (1.01)2×218+(1.01)2×2-5 |
| エ | (1.001)2×220+(1.1111)2×221 |
令和4年7月修了試験 問3
2桁の2進数 x1x2 が表す整数をxとする。2進数 x2x1 が表す整数を,xの式で表したものはどれか。ここで,int(r) は非負の実数の小数点以下を切り捨てた整数を表す。
| ア | |
|---|---|
| イ | |
| ウ | |
| エ |
令和4年6月修了試験 問1
| ア | 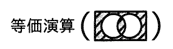 |
|---|---|
| イ |  |
| ウ |  |
| エ |  |
答え : ア
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
令和4年1月修了試験 問1
0以上65,536未満の整数xを,16ビットの2進数で表現して,上位8ビットと下位8ビットを入れ替える。得られたピット列を2進数とみなしたとき,その値をxを用いた式で表したものはどれか。ここで,a÷b はaをbで割った商の整数部分を,a%b はaをbで割った余りを表す。また,式の中の数値は10進数である。
| ア | (x÷256)+(x%256) |
|---|---|
| イ | (x÷256)+(x%256)×256 |
| ウ | (x÷256)×256+(x%256) |
| エ | (x÷256)×256+(x%256)×256 |
令和3年12月修了試験 問1
nビットの値L1,L2がある。次の操作によって得られる値L3は,L1とL2に対するどの論理演算の結果と同じか。
〔操作〕
(1)L1とL2のビットごとの論理和をとって,変数Xに記憶する。
(2)L1とL2のビットごとの論理積をとって更に否定をとり,変数Yに記憶する。
(3)XとYのビットごとの論理積をとって,結果をL3とする。
〔操作〕
(1)L1とL2のビットごとの論理和をとって,変数Xに記憶する。
(2)L1とL2のビットごとの論理積をとって更に否定をとり,変数Yに記憶する。
(3)XとYのビットごとの論理積をとって,結果をL3とする。
| ア | 排他的論理和 |
|---|---|
| イ | 排他的論理和の否定 |
| ウ | 論理積の否定 |
| エ | 論理和の否定 |
答え : ア
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
令和3年7月修了試験 問1
次に示す手順は,列中の少なくとも一つは1であるビット列が与えられたとき,最も右にある1を残し,他のビットを全て0にするアルゴリズムである。例えば,00101000が与えられたとき,00001000が求まる。aに入る論理演算はどれか。
手順1 与えられたビット列Aを符号なしの2進数と見なし,Aから1を引き,結果をBとする。
手順2 AとBの排他的論理和(XOR)を求め,結果をCとする。
手順3 AとCの [ a ] を求め,結果をAとする。
手順1 与えられたビット列Aを符号なしの2進数と見なし,Aから1を引き,結果をBとする。
手順2 AとBの排他的論理和(XOR)を求め,結果をCとする。
手順3 AとCの [ a ] を求め,結果をAとする。
| ア | 排他的論理和(XOR) |
|---|---|
| イ | 否定論理積(NAND) |
| ウ | 論理積(AND) |
| エ | 論理和(OR) |
令和3年7月修了試験 問4
ある工場では,同じ製品を独立した二つのラインA,Bで製造している。ラインAでは製品全体の60%を製造し,ラインBでは40%を製造している。ラインAで製造された製品の2%が不良品であり,ラインBで製造された製品の1%が不良品であることが分かっている。いま,この工場で製造された製品の一つを無作為に抽出して調べたところ,それは不良品であった。その製品がラインAで製造された確率は何%か。
| ア | 40 |
|---|---|
| イ | 50 |
| ウ | 60 |
| エ | 75 |
令和3年1月修了試験 問2
| ア | |
|---|---|
| イ | |
| ウ | |
| エ |
令和2年12月修了試験 問3
| ア | 16進表記0Fのビット列との排他的論理和をとる。 |
|---|---|
| イ | 16進表記0Fのビット列との否定論理積をとる。 |
| ウ | 16進表記0Fのビット列との論理積をとる。 |
| エ | 16進表記0Fのビット列との論理和をとる。 |
令和2年6月修了試験 問2
| ア | (A∪B)∩(A∩C)= B ∩(A∪C) |
|---|---|
| イ | (A∪B)∩ C = (A∪C)∩(B∪C) |
| ウ | (A∩C)∪(B∩A)=(A∩B)∪(B∩C) |
| エ | (A∩C)∪(B∩C)=(A∪B)∩ C |
令和2年1月修了試験 問1
| ア | -(2n-1-1) |
|---|---|
| イ | -1 |
| ウ | 0 |
| エ | 2n-1 |
令和1年12月修了試験 問2
実数aを a = f×re と表す浮動小数点表示に関する記述として,適切なものはどれか。
| ア | fを仮数,eを指数,rを基数という。 |
|---|---|
| イ | fを基数,eを仮数,rを指数という。 |
| ウ | fを基数,eを指数,rを仮数という。 |
| エ | fを指数,eを基数,rを仮数という。 |
令和1年秋期 問2
| ア | 16進表記00のビット列と排他的論理和をとる。 |
|---|---|
| イ | 16進表記00のビット列と論理和をとる。 |
| ウ | 16進表記FFのビット列と排他的論理和をとる。 |
| エ | 16進表記FFのビット列と論理和をとる。 |
答え : ウ
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
令和1年7月修了試験 問1
| ア | xを2ビット左にシフトした値にxを加算し,更に1ビット左にシフトする。 |
|---|---|
| イ | xを2ビット左にシフトした値にxを加算し,更に2ビット左にシフトする。 |
| ウ | xを3ビット左にシフトした値と,xを2ビット左にシフトした値を加算する。 |
| エ | xを3ビット左にシフトした値にxを加算し,更に1ビット左にシフトする。 |
令和1年7月修了試験 問2
負の整数を表現する代表的な方法として,次の3種類がある。
a 1の補数による表現
b 2の補数による表現
c 絶対値に符号を付けた表現(左端ビットが0の場合は正,1の場合は負)
4ビットのパターン 1101 を a~c の方法で表現したものと解釈したとき,値が小さい順になるように三つの方法を並べたものはどれか。
a 1の補数による表現
b 2の補数による表現
c 絶対値に符号を付けた表現(左端ビットが0の場合は正,1の場合は負)
4ビットのパターン 1101 を a~c の方法で表現したものと解釈したとき,値が小さい順になるように三つの方法を並べたものはどれか。
| ア | a,c,b |
|---|---|
| イ | b,a,c |
| ウ | b,c,a |
| エ | c,b,a |
令和1年7月修了試験 問3
| ア | A・B・C |
|---|---|
| イ | A・B・C+A・B・C |
| ウ | A・B+B・C |
| エ | C |
令和1年6月修了試験 問1
次の10進小数のうち,8進数に変換したときに有限小数になるものはどれか。
| ア | 0.3 |
|---|---|
| イ | 0.4 |
| ウ | 0.5 |
| エ | 0.8 |
平成30年12月修了試験 問1
| ア | 0.01 |
|---|---|
| イ | 0.02 |
| ウ | 0.05 |
| エ | 0.08 |
平成30年12月修了試験 問2
XとYの否定論理積 X NAND Y は,NOT(X AND Y) として定義される。X OR Y をNANDだけを使って表した論理式はどれか。
| ア | ((X NAND Y) NAND X) NAND Y |
|---|---|
| イ | (X NAND X) NAND (Y NAND Y) |
| ウ | (X NAND Y) NAND (X NAND Y) |
| エ | X NAND (Y NAND (X NAND Y)) |
平成30年7月修了試験 問1
非負の2進数 b1b2…bn を3倍にしたものはどれか。
| ア | b1b2…bn0+b1b2…bn |
|---|---|
| イ | b1b2…bn00-1 |
| ウ | b1b2…bn000 |
| エ | b1b2…bn1 |
平成30年7月修了試験 問2
| ア | 8 |
|---|---|
| イ | 16 |
| ウ | 128 |
| エ | 256 |
平成30年春期 問1
ある整数値を,負数を2の補数で表現する2進表記法で表すと最下位2ビットは “11” であった。10進表記法の下で,その整数値を4で割ったときの余りに関する記述として,適切なものはどれか。ここで,除算の商は,絶対値の小数点以下を切り捨てるものとする。
| ア | その整数値が正ならば3 |
|---|---|
| イ | その整数値が負ならば-3 |
| ウ | その整数値が負ならば3 |
| エ | その整数値の正負にかかわらず0 |
答え : ア
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
平成30年1月修了試験 問2
| ア | 1011 |
|---|---|
| イ | 1100 |
| ウ | 1101 |
| エ | 1110 |
答え : エ
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
平成29年12月修了試験 問3
| ア | (A∩B)⊆C |
|---|---|
| イ | (A∩B)⊆C |
| ウ | (A∩B)⊆C |
| エ | (A∩B)⊆C |
答え : エ
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
平成29年1月修了試験 問1
16進小数 2A.4C を10進小数に変換したものはどれか。
| ア | 25+23+21+2-2+2-5+2-6 |
|---|---|
| イ | 25+23+21+2-1+2-4+2-5 |
| ウ | 26+24+22+2-2+2-5+2-6 |
| エ | 26+24+22+2-1+2-4+2-5 |
平成27年12月修了試験 問2
浮動小数点形式で表現される数値の演算において,有効桁数が大きく減少するものはどれか。
| ア | 絶対値がほぼ等しく,同符号である数値の加算 |
|---|---|
| イ | 絶対値がほぼ等しく,同符号である数値の減算 |
| ウ | 絶対値の大きな数と絶対値の小さな数の加算 |
| エ | 絶対値の大きな数と絶対値の小さな数の減算 |
平成27年7月修了試験 問2
| ア | xと2進数 00001111 のビットごとの論理積をとった結果が0である。 |
|---|---|
| イ | xと2進数 00001111 のビットごとの論理和をとった結果が0である。 |
| ウ | xと2進数 11110000 のビットごとの論理積をとった結果が0である。 |
| エ | xと2進数 11110000 のビットごとの論理和をとった結果が0である。 |
答え : ア
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
平成27年6月修了試験 問1
16進数0.75と等しいものはどれか。
| ア | 2-2+2-5+2-7+2-8 |
|---|---|
| イ | 2-2+2-3+2-4+2-6+2-8 |
| ウ | 2-1+2-2 |
| エ | 2-1+2-2+2-3+2-4+2-6 |
平成27年6月修了試験 問2
| ア | 01001100 |
|---|---|
| イ | 10100101 |
| ウ | 10100110 |
| エ | 11010011 |
平成27年1月修了試験 問1
16ビットの2進数nを16進数の各桁に分けて,下位の桁から順にスタックに格納するために,次の手順を4回繰り返す。a,bに入る適切な語句の組合せはどれか。ここで,XXXX16 は16進数XXXXを表す。
〔手順〕
(1)[ a ] をxに代入する。
(2)xをスタックにプッシュする。
(3)nを [ b ] 論理シフトする。
〔手順〕
(1)[ a ] をxに代入する。
(2)xをスタックにプッシュする。
(3)nを [ b ] 論理シフトする。
| a | b | |
| ア | n AND 000F16 | 左に4ビット |
| イ | n AND 000F16 | 右に4ビット |
| ウ | n AND FFF016 | 左に4ビット |
| エ | n AND FFF016 | 右に4ビット |
平成26年12月修了試験 問1
正の整数の10進表示の桁数Dと2進表示の桁数Bとの関係を表す式のうち,最も適切なものはどれか。
| ア | D ≒ 2 log10 B |
|---|---|
| イ | D ≒ 10 log2 B |
| ウ | D ≒ B log2 10 |
| エ | D ≒ B log10 2 |
答え : エ
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
平成26年12月修了試験 問2
NOR(否定論理和)は2項論理演算の一つである。x NOR y の行に入る結果はどれか。
| x | 0 0 1 1 |
| y | 0 1 0 1 |
| x NOR y |
| ア | 0 1 1 0 |
| イ | 1 0 0 0 |
| ウ | 1 0 0 1 |
| エ | 1 1 1 0 |
答え : イ
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
平成26年12月修了試験 問3
| ア | 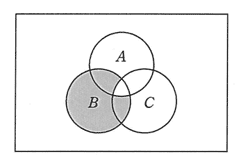 |
|---|---|
| イ | 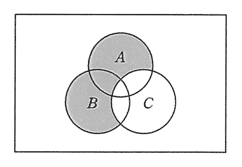 |
| ウ | 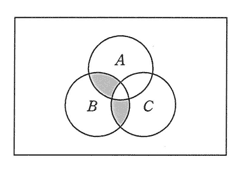 |
| エ | 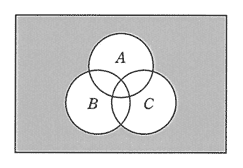 |
平成26年秋期 問2
0000~4999 のアドレスをもつハッシュ表があり,レコードのキー値からアドレスに変換するアルゴリズムとして基数変換法を用いる。キー値が55550のときのアドレスはどれか。ここでの基数変換法は,キー値を11進数とみなし,10進数に変換した後,下4桁に対して0.5を乗じた結果(小数点以下は切捨て)をレコードのアドレスとする。
| ア | 0260 |
|---|---|
| イ | 2525 |
| ウ | 2775 |
| エ | 4405 |
平成26年7月修了試験 問2
1ビットの数 A,B の和を2ビットで表現したとき,上位ビットCと下位ビットSを表す論理式の組合せはどれか。ここで,“・” は論理積,“+” は論理和,XはXの否定を表す。
| A | B | AとBの和 | |
| C | S | ||
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
| C | S | |
| ア | A・B | (A・B)+(A・B) |
| イ | A・B | (A+B)・(A+B) |
| ウ | A+B | (A・B)+(A・B) |
| エ | A+B | (A+B)・(A+B) |
答え : ア
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
平成26年6月修了試験 問1
次の計算は何進法で成立するか。
131 - 45 = 53
131 - 45 = 53
| ア | 6 |
|---|---|
| イ | 7 |
| ウ | 8 |
| エ | 9 |
平成25年12月修了試験 問2
| ア | 120 |
|---|---|
| イ | 127 |
| ウ | 170 |
| エ | 240 |
答え : エ
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
平成25年秋期 問2
| ア | 2AF3 |
|---|---|
| イ | 6AF3 |
| ウ | AF34 |
| エ | EAF3 |
答え : ア
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
平成25年7月修了試験 問2
内部鍵との排他的論理和を4ビット単位で実行するユニットA,B,Cから構成される装置がある。この装置では,入力ビット列 1101 を与えると,出力ビット列 0100 が得られる。ここで,ユニットBの内部鍵を変更したところ,出力ビット列が 1111 になった。変更後のユニットBの内部鍵はどれか。


| ア | 1011 |
|---|---|
| イ | 1100 |
| ウ | 1101 |
| エ | 1110 |
平成25年7月修了試験 問4
| ア |
| |||
|---|---|---|---|---|
| イ |
| |||
| ウ |
| |||
| エ |
|
答え : エ
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
平成25年6月修了試験 問2
次の真理値表で,変数X,Y,Zに対する関数Fを表す式はどれか。ここで,“・”は論理積,“+”は論理和,AはAの否定を表す。
| X Y Z | F |
|
0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 |
0 1 1 0 0 0 1 1 |
| ア | X・Y・Z+X・Y+Y・Z |
|---|---|
| イ | X・Y・Z+X・Y+Y・Z |
| ウ | X・Y・Z+Y |
| エ | X・Y+Y・Z |
答え : ア
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
平成25年6月修了試験 問4
| ア | 16 |
|---|---|
| イ | 24 |
| ウ | 70 |
| エ | 128 |
答え : ウ
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
平成24年12月修了試験 問1
| ア | A⊆(A∩B) |
|---|---|
| イ | (A∪B)⊆(A∪B) |
| ウ | (A∩B)⊆(A∪B) |
| エ | (A∩B)⊆(A∩B) |
答え : ウ
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
平成24年12月修了試験 問2
| ア | (n OR 10000000)+ 00000001 |
|---|---|
| イ | (n OR 11111110)+ 11111111 |
| ウ | (n XOR 10000000)+ 11111111 |
| エ | (n XOR 11111111)+ 00000001 |
答え : エ
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
平成24年秋期 問1
| ア | 00001000 |
|---|---|
| イ | 00011111 |
| ウ | 00100000 |
| エ | 11100000 |
答え : ウ
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
平成24年7月修了試験 問2
| ア | 3FFFFF |
|---|---|
| イ | 7FFFFF |
| ウ | BFFFFF |
| エ | FFFFFF |
答え : イ
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
平成24年6月修了試験 問1
16進小数 0.FEDC を4倍したものはどれか。
| ア | 1.FDB8 |
|---|---|
| イ | 2.FB78 |
| ウ | 3.FB70 |
| エ | F.EDC0 |
答え : ウ
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
平成24年1月修了試験 問3
| ア | -22~2n-1 |
|---|---|
| イ | -2n-1-1~2n-1 |
| ウ | -2n-1~2n-1-1 |
| エ | -2n-1~2n-1 |
答え : ウ
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
平成23年7月修了試験 問2
| ア | -115 |
|---|---|
| イ | -3 |
| ウ | -2 |
| エ | 27 |
答え : イ
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
平成23年1月修了試験 問2
| ア | 16進数03と排他的論理和をとる。 |
|---|---|
| イ | 16進数03と論理和をとる。 |
| ウ | 16進数FCと排他的論理和をとる。 |
| エ | 16進数FCと論理和をとる。 |
答え : ウ
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
平成22年12月修了試験 問1
| ア | |
|---|---|
| イ | |
| ウ | |
| エ |
答え : ウ
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
平成21年12月修了試験 問3
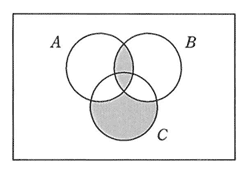
ワープロソフト,表計算ソフト,データベースソフトが使える人数を調査して図1のように図示した。これにプレゼンテーションソフトが使える人数の調査結果を加えて,図2のように図示しようとしたところ,うまくいかないことが分かった。図2において表されていないケースはどれか。解答群ではワープロソフト,表計算ソフト,データベースソフト,プレゼンテーションソフトをそれぞれW,H,D,Pで表し,○は使えることを,×は使えないことを示している。
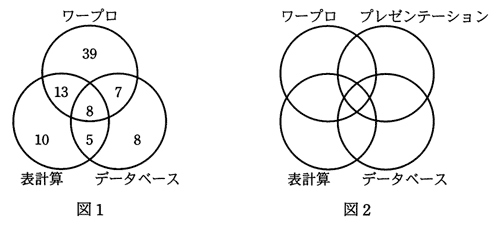

| W | H | D | P | |
| ア | ○ | ○ | ○ | ○ |
| イ | ○ | ○ | ○ | × |
| ウ | ○ | × | ○ | × |
| エ | ○ | × | × | × |
答え : ウ
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
平成21年6月修了試験 問1
次の計算は何進法で成立するか。
1015÷5 = 131(余り0)
1015÷5 = 131(余り0)
| ア | 6 |
|---|---|
| イ | 7 |
| ウ | 8 |
| エ | 9 |
答え : イ
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学