ハフマン符号【Huffman code】ハフマン符号化 / Huffman coding / ハフマン圧縮 / Huffman compression

概要

ハフマン符号（Huffman code）とは、1952年にデビット・ハフマン(David Albert Huffman)氏が考案した、データ圧縮方式。代表的な可逆圧縮符号の一つで、現代でもファイル圧縮や画像ファイル形式など様々な場面で応用されている。

データの内容を損なわずに短い符号列に変換する圧縮アルゴリズムの一つで、符号化方式を「ハフマン符号化」（Huffman coding）、得られる圧縮符号を「ハフマン符号」（Huffman code）という。圧縮符号を展開すると完全に元通りのデータを復元することができる可逆圧縮である。

基本的な考え方は、対象データ列に出現する各パターンの頻度を調べ、高頻度で現れるパターンには短い符号（ビット列）を、低頻度のパターンには長い符号を割り当てることで全体のデータ長を短縮する。このような圧縮符号を「エントロピー符号」という。

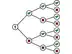
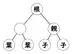
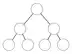
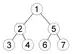
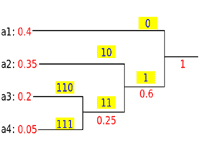
ハフマン符号ではデータ全体を一定の長さの断片ごとに区切り、同じパターンの断片の出現回数を数え上げる。最も頻出するものから順に短い符号を割り当て、パターンを符号に置き換える。置換後の符号列中で各符号を一意に識別できるようにするため、「ハフマン木」と呼ばれる二分木でパターンと符号の対応関係を管理する。

符号化のためにはパターンの出現頻度を調べる必要があるが、最初に出現頻度をすべて調べて符号の割り当てを決めてから符号化を行う方式（データ全体を2回走査する）を「静的ハフマン符号」（static Huffman coding）、出現頻度を調べ符号の割り当てを変更しながら同時に符号化を進めていく方式（一度の走査で済む）を「適応的ハフマン符号」（adaptive Huffman coding）という。

実装が難しく、かつては特許で保護されていた「算術符号」（arithmetic coding）を除けば、理論上最も圧縮率が高いエントロピー符号化アルゴリズムとして知られる。実装も比較的容易であることから、Zip（Deflate）やJPEG、MP3など様々な圧縮形式の仕様の一部に採用され、広く普及している。

(2024.3.11更新)