基本情報技術者(科目A)過去問集 - アルゴリズム
令和7年6月修了試験 問6
データの整列方法に関する記述のうち,適切なものはどれか。
| ア | クイックソートでは,ある一定間隔おきに取り出した要素から成る部分列をそれぞれ整列し,更に間隔を詰めて同様の操作を行い,間隔が1になるまでこれを繰り返す。 |
|---|---|
| イ | シェルソートでは,隣り合う要素を比較して,大小の順が逆であれば,それらの要素を入れ替えるという操作を繰り返す。 |
| ウ | バブルソートでは,中間的な基準値を決めて,それよりも大きな値を集めた区分と小さな値を集めた区分に要素を振り分ける。次に,それぞれの区分の中で同様な処理を繰り返す。 |
| エ | ヒープソートでは,未整列の部分を順序木に構成し,そこから最大値又は最小値を取り出して既整列の部分に移す。この操作を繰り返して,未整列部分を縮めていく。 |
令和7年1月修了試験 問6
| ア | 1回増える。 |
|---|---|
| イ | 2回増える。 |
| ウ | 約2倍になる。 |
| エ | 約4倍になる。 |
令和6年12月修了試験 問4
関数f(x)は,引数も戻り値も実数型である。この関数を使った,①〜⑤から成る手続を考える。手続の実行を開始してから②~⑤を十分に繰り返した後に,③で表示されるyの値に変化がなくなった。このとき成立する関係式はどれか。
① x ← a
② y ← f(x)
③ yの値を表示する。
④ x ← y
⑤ ②に戻る。
① x ← a
② y ← f(x)
③ yの値を表示する。
④ x ← y
⑤ ②に戻る。
| ア | f(a) = y |
|---|---|
| イ | f(y) = 0 |
| ウ | f(y) = a |
| エ | f(y) = y |
令和6年12月修了試験 問6
アルファベット3文字で構成されるキーがある。次の式によってハッシュ値hを決めるとき,キー “SEP” と衝突するのはどれか。ここで,a mod b は,aをbで割った余りを表す。
h = (キーの各アルファベットの順位の総和) mod 27
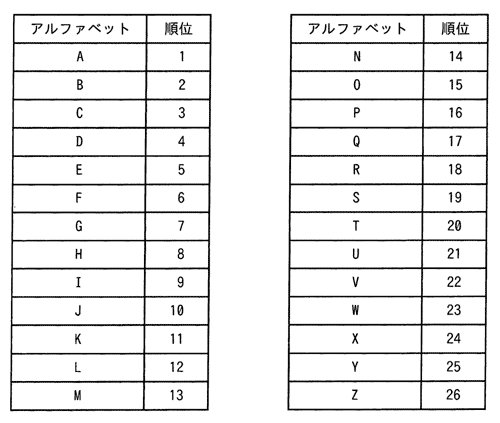
h = (キーの各アルファベットの順位の総和) mod 27

| ア | APR |
|---|---|
| イ | FEB |
| ウ | JAN |
| エ | NOV |
令和6年7月修了試験 問6
| ア | log2n |
|---|---|
| イ | (log2n+1)/2 |
| ウ | n |
| エ | n2 |
令和6年6月修了試験 問6
| ア | 対象集合から基準となる要素を選び,これよりも大きい要素の集合と小さい要素の集合に分割する。この操作を繰り返すことによって,整列を行う。 |
|---|---|
| イ | 対象集合から最も小さい要素を順次取り出して,整列を行う。 |
| ウ | 対象集合から要素を順次取り出し,それまでに取り出した要素の集合に順序関係を保つよう挿入して,整列を行う。 |
| エ | 隣り合う要素を比較し,逆順であれば交換して,整列を行う。 |
令和6年公開問題 問2
キーが小文字のアルファベット1文字(a,b,…,z のいずれか)であるデータを,大きさが10のハッシュ表に格納する。ハッシュ関数として,アルファベットのASCIIコードを10進表記法で表したときの1の位の数を用いることにする。衝突が起こるキーの組合せはどれか。ASCIIコードでは,昇順に連続した2進数が,アルファベット順にコードとして割り当てられている。
| ア | a と i |
|---|---|
| イ | b と r |
| ウ | c と l |
| エ | d と x |
令和5年7月修了試験 問15
ハッシュ法の説明として,適切なものはどれか。
| ア | 関数を用いてレコードのキー値からレコードの格納アドレスを求めることによってアクセスする方法 |
|---|---|
| イ | それぞれのレコードに格納されている次のレコードの格納アドレスを用いることによってアクセスする方法 |
| ウ | レコードのキー値とレコードの格納アドレスの対応表を使ってアクセスする方法 |
| エ | レコードのキー値をレコードの格納アドレスとして直接アクセスする方法 |
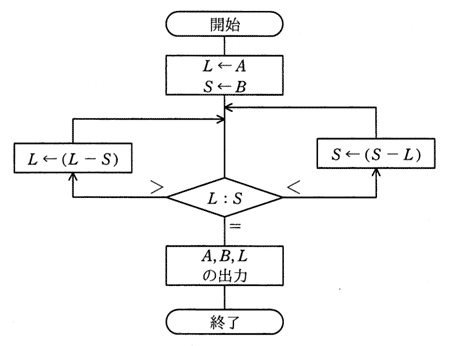
令和5年公開問題 問11
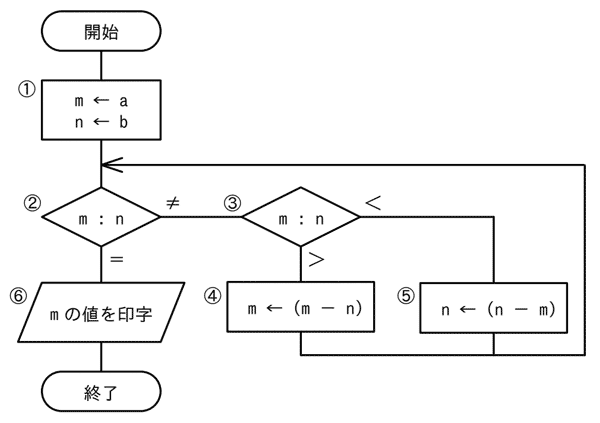
次の流れ図において,
① → ② → ③ → ⑤ → ② → ③ → ④ → ② → ⑥
の順に実行させるために,①においてmとnに与えるべき初期値aとbの関係はどれか。ここで,a,bはともに正の整数とする。
① → ② → ③ → ⑤ → ② → ③ → ④ → ② → ⑥
の順に実行させるために,①においてmとnに与えるべき初期値aとbの関係はどれか。ここで,a,bはともに正の整数とする。

| ア | a = 2b |
|---|---|
| イ | 2a = b |
| ウ | 2a = 3b |
| エ | 3a = 2b |
令和5年1月修了試験 問8
次の関数 f(n,k) がある。f(4,2) の値は幾らか。
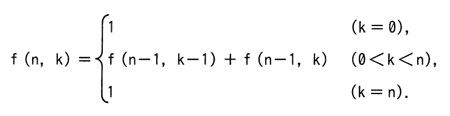
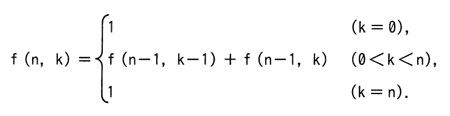
| ア | 3 |
|---|---|
| イ | 4 |
| ウ | 5 |
| エ | 6 |
令和5年1月修了試験 問9
異なるn個のデータが昇順に整列された表がある。この表をm個のデータごとのブロックに分割し,各ブロックの最後尾のデータだけを線形探索することによって,目的のデータの存在するブロックを探し出す。次に,当該ブロック内を線形探索して目的のデータを探し出す。このときの平均比較回数を表す式はどれか。ここで,mは十分に大きく,nはmの倍数とし,目的のデータは必ず表の中に存在するものとする。
| ア | |
|---|---|
| イ | |
| ウ | |
| エ |
答え : イ
分野 : テクノロジ系 › 基礎理論 › アルゴリズムとプログラミング › アルゴリズム
分野 : テクノロジ系 › 基礎理論 › アルゴリズムとプログラミング › アルゴリズム
令和4年12月修了試験 問8
バブルソートの説明として,適切なものはどれか。
| ア | ある間隔おきに取り出した要素から成る部分列をそれぞれ整列し,更に間隔を詰めて同様の操作を行い,間隔が1になるまでこれを繰り返す。 |
|---|---|
| イ | 中間的な基準値を決めて,それよりも大きな値を集めた区分と,小さな値を集めた区分に要素を振り分ける。次に,それぞれの区分の中で同様の操作を繰り返す。 |
| ウ | 隣り合う要素を比較して,大小の順が逆であれば,それらの要素を入れ替えるという操作を繰り返す。 |
| エ | 未整列の部分を順序木にし,そこから最小値を取り出して整列済の部分に移す。この操作を繰り返して,未整列の部分を縮めていく。 |
答え : ウ
分野 : テクノロジ系 › 基礎理論 › アルゴリズムとプログラミング › アルゴリズム
分野 : テクノロジ系 › 基礎理論 › アルゴリズムとプログラミング › アルゴリズム
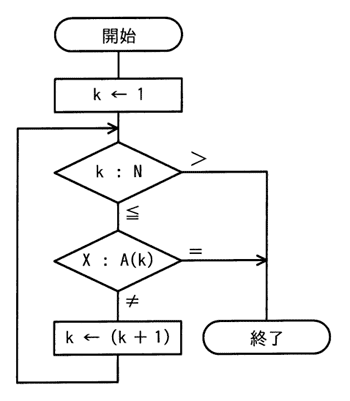
令和4年12月修了試験 問9
| ア | Xと同じ値が配列中にない場合,kには1が設定されている |
|---|---|
| イ | Xと同じ値が配列中にない場合,kにはNが設定されている。 |
| ウ | Xと同じ値が配列の1番目とN番目の2か所にある場合,kには1が設定されている。 |
| エ | Xと同じ値が配列の1番目とN番目の2か所にある場合,kにはNが設定されている。 |
令和4年12月修了試験 問10
| ア | 6 |
|---|---|
| イ | 9 |
| ウ | 15 |
| エ | 25 |
令和4年7月修了試験 問10
整数x,y(x>y≧0)に対して,次のように定義された関数F(x,y)がある。F(231,15)の値は幾らか。ここで,x mod yはxをyで割った余りである。
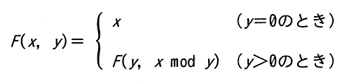
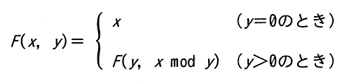
| ア | 2 |
|---|---|
| イ | 3 |
| ウ | 5 |
| エ | 7 |
令和4年6月修了試験 問5
与えられた正の整数 x0,x1(x0>x1)の最大公約数を,次の手順で求める。x0=175,x1=77の場合,手順(2)は何回実行するか。ここで,“A←B” は,BをAに代入することを表す。
〔手順〕
(1)i ← 2
(2)xi ← “xi-2をxi-1で割った剰余”
(3)xi=0 ならばxi-1を最大公約数として終了する。
(4)“i ← i+1” として(2)に戻る。
〔手順〕
(1)i ← 2
(2)xi ← “xi-2をxi-1で割った剰余”
(3)xi=0 ならばxi-1を最大公約数として終了する。
(4)“i ← i+1” として(2)に戻る。
| ア | 3 |
|---|---|
| イ | 4 |
| ウ | 6 |
| エ | 7 |
令和4年6月修了試験 問7
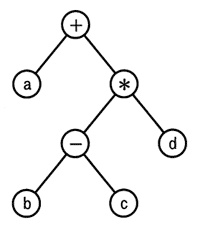
2分木の各ノードがもつ記号を出力する再帰的なプログラムProc(n)の定義は,次のとおりである。このプログラムを,図の2分木の根(最上位のノード)に適用したときの出力はどれか。
Proc(n){
nに左の子 l があればProc(l)を呼び出す。
nに右の子 r があればProc(r)を呼び出す。
nの記号を出力して終了する。
}
Proc(n){
nに左の子 l があればProc(l)を呼び出す。
nに右の子 r があればProc(r)を呼び出す。
nの記号を出力して終了する。
}

| ア | +a*-bcd |
|---|---|
| イ | a+b-c*d |
| ウ | abc-d*+ |
| エ | b-c*d+a |
令和4年6月修了試験 問9
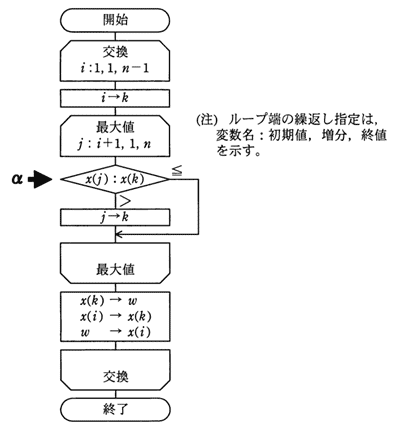
配列 A[i](i=1,2,...,n) を,次のアルゴリズムによって整列する。行2~3の処理が初めて終了したとき,必ず実現されている配列の状態はどれか。
〔アルゴリズム〕
行番号
1 iを1からn-1まで1ずつ増やしながら行2~3を繰り返す
2 jをnからi+1まで1ずつ減らしながら行3を繰り返す
3 もし A[j]<A[j-1] ならば,A[j]とA[j-1]を交換する
〔アルゴリズム〕
行番号
1 iを1からn-1まで1ずつ増やしながら行2~3を繰り返す
2 jをnからi+1まで1ずつ減らしながら行3を繰り返す
3 もし A[j]<A[j-1] ならば,A[j]とA[j-1]を交換する
| ア | A[1]が最小値になる。 |
|---|---|
| イ | A[1]が最大値になる。 |
| ウ | A[n]が最小値になる。 |
| エ | A[n]が最大値になる。 |
令和4年6月修了試験 問10
| ア | n<M |
|---|---|
| イ | n>M-1 |
| ウ | n>M |
| エ | n>M+1 |
令和4年1月修了試験 問9
再帰的に定義された手続 proc で,proc(5)を実行したとき,印字される数字を順番に並べたものはどれか。
proc(n)
n=0 ならば戻る
そうでなければ
{
nを印字する
proc(n-1)を呼び出す
nを印字する
}
を実行して戻る
proc(n)
n=0 ならば戻る
そうでなければ
{
nを印字する
proc(n-1)を呼び出す
nを印字する
}
を実行して戻る
| ア | 543212345 |
|---|---|
| イ | 5432112345 |
| ウ | 54321012345 |
| エ | 543210012345 |
令和3年12月修了試験 問8
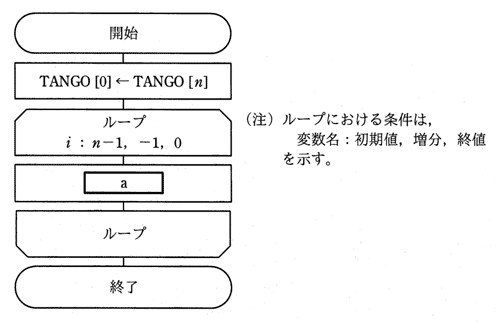
要素番号が0から始まる配列 TANGO がある。n個の単語が TANGO[1] から TANGO[n] に入っている。図は,n番目の単語を TANGO[1] に移動するために,TANGO[1] から TANGO[n-1] の単語を順に一つずつ後ろにずらして単語表を再構成する流れ図である。aに入れる処理として,適切なものはどれか。

| ア | TANGO[i] ← TANGO[n-i] |
|---|---|
| イ | TANGO[i+1] ← TANGO[i] |
| ウ | TANGO[n-i] ← TANGO[i] |
| エ | TANGO[n-i] ← TANGO[i+1] |
令和3年7月修了試験 問9
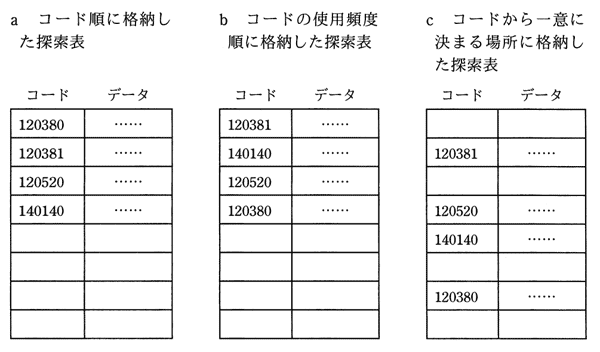
探索表の構成法を例とともに a〜c に示す。最も適した探索手法の組合せはどれか。ここで,探索表のコードの空欄は表の空きを示す。

| a | b | c | |
| ア | 2分探索 | 線形探索 | ハッシュ表探索 |
| イ | 2分探索 | ハッシュ表探索 | 線形探索 |
| ウ | 線形探索 | 2分探索 | ハッシュ表探索 |
| エ | 線形探索 | ハッシュ表探索 | 2分探索 |
答え : ア
分野 : テクノロジ系 › 基礎理論 › アルゴリズムとプログラミング › アルゴリズム
分野 : テクノロジ系 › 基礎理論 › アルゴリズムとプログラミング › アルゴリズム
令和3年7月修了試験 問10
| ア | n+F(n-1) |
|---|---|
| イ | n-1+F(n) |
| ウ | n×F(n-1) |
| エ | (n-1)×F(n) |
令和3年6月修了試験 問8
自然数をキーとするデータを,ハッシュ表を用いて管理する。キーxのハッシュ関数 h(x) を
h(x) = x mod n
とすると,任意のキーaとbが衝突する条件はどれか。ここで,nはハッシュ表の大きさであり,x mod nはxをnで割った余りを表す。
h(x) = x mod n
とすると,任意のキーaとbが衝突する条件はどれか。ここで,nはハッシュ表の大きさであり,x mod nはxをnで割った余りを表す。
| ア | a+bがnの倍数 |
|---|---|
| イ | a-bがnの倍数 |
| ウ | nがa+bの倍数 |
| エ | nがa-bの倍数 |
答え : イ
分野 : テクノロジ系 › 基礎理論 › アルゴリズムとプログラミング › アルゴリズム
分野 : テクノロジ系 › 基礎理論 › アルゴリズムとプログラミング › アルゴリズム
令和3年6月修了試験 問9
関数 f(x,y) が次のとおり定義されているとき,f(775,527) の値は幾らか。ここで,x mod y はxをyで割った余りを返す。
f(x,y):if y = 0 then return x else return f(y,x mod y)
f(x,y):if y = 0 then return x else return f(y,x mod y)
| ア | 0 |
|---|---|
| イ | 31 |
| ウ | 248 |
| エ | 527 |
令和3年6月修了試験 問10
xとyを自然数とするとき,流れ図で表される手続を実行した結果として,適切なものはどれか。
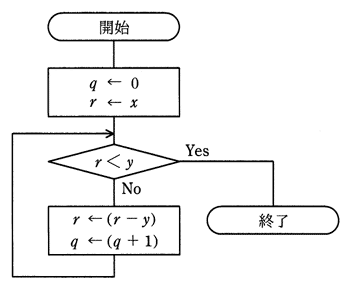

| qの値 | rの値 | |
| ア | x÷yの余り | x÷yの商 |
| イ | x÷yの商 | x÷yの余り |
| ウ | y÷xの余り | y÷xの商 |
| エ | y÷xの商 | y÷xの余り |
令和3年1月修了試験 問10
| ア | 4 |
|---|---|
| イ | 9 |
| ウ | 10 |
| エ | 11 |
令和2年12月修了試験 問1
次の流れ図は,10進整数j(0<j<100)を8桁の2進数に変換する処理を表している。2進数は下位桁から順に,配列の要素 NISHIN(1) から NISHIN(8) に格納される。流れ図のa及びbに入れる処理はどれか。ここで,j div 2 はjを2で割った商の整数部分を,j mod 2はjを2で割った余りを表す。
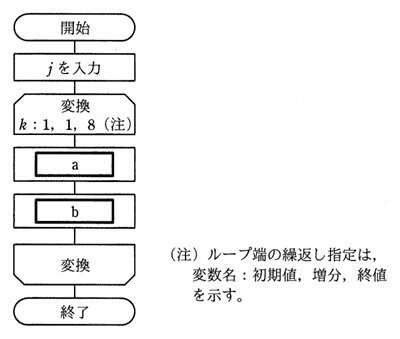

| a | b | |
| ア | j ← j div 2 | NISHIN(k) ← j mod 2 |
| イ | j ← j mod 2 | NISHIN(k) ← j div 2 |
| ウ | NISHIN(k) ← j div 2 | j ← j mod 2 |
| エ | NISHIN(k) ← j mod 2 | j ← j div 2 |
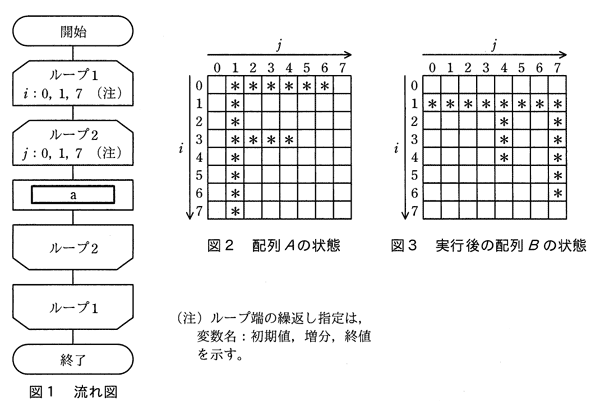
令和2年12月修了試験 問8
| ア | B(7-i,7-j) ← A(i,j) |
|---|---|
| イ | B(7-j,i) ← A(i,j) |
| ウ | B(i,7-j) ← A(i,j) |
| エ | B(j,7-i)←A(i,j) |
令和2年12月修了試験 問10
顧客番号をキーとして顧客データを検索する場合,2分探索を使用するのが適しているものはどれか。
| ア | 顧客番号から求めたハッシュ値が指し示す位置に配置されているデータ構造 |
|---|---|
| イ | 顧客番号に関係なく,ランダムに配置されているデータ構造 |
| ウ | 顧客番号の昇順に配置されているデータ構造 |
| エ | 顧客番号をセルに格納し,セルのアドレス順に配置されているデータ構造 |
令和2年7月修了試験 問4
0≦x≦1 の範囲で単調に増加する連続関数 f(x) が f(0)<0≦f(1) を満たすときに,区間内で f(x)=0 であるxの値を近似的に求めるアルゴリズムにおいて,(2)は何回実行されるか。
〔アルゴリズム〕
(1)x0 ← 0,x1 ← 1とする。
(2)x ← とする。
(3)x1 - x < 0.001 ならばxの値を近似値として終了する。
(4)f(x)≧0 ならば x1 ← x として,そうでなければ x0 ← x とする。
(5)(2)に戻る。
〔アルゴリズム〕
(1)x0 ← 0,x1 ← 1とする。
(2)x ← とする。
(3)x1 - x < 0.001 ならばxの値を近似値として終了する。
(4)f(x)≧0 ならば x1 ← x として,そうでなければ x0 ← x とする。
(5)(2)に戻る。
| ア | 10 |
|---|---|
| イ | 20 |
| ウ | 100 |
| エ | 1,000 |
答え : ア
分野 : テクノロジ系 › 基礎理論 › アルゴリズムとプログラミング › アルゴリズム
分野 : テクノロジ系 › 基礎理論 › アルゴリズムとプログラミング › アルゴリズム
令和2年6月修了試験 問10
長さ m,n の文字列をそれぞれ格納した配列 X,Y がある。図は,配列Xに格納した文字列の後ろに,配列Yに格納した文字列を連結したものを,配列に格納するアルゴリズムを表す流れ図である。図中の a,b に入れる処理として,適切なものはどれか。ここで,1文字が一つの配列要素に格納されるものとする。
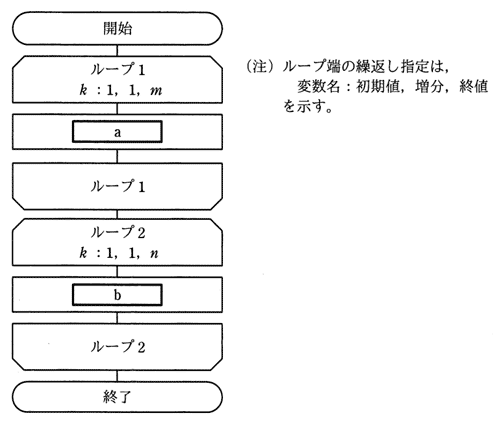

| a | b | |
| ア | Z(k) ← X(k) | Z(m+k) ← Y(k) |
| イ | Z(k) ← X(k) | Z(n+k) ← Y(k) |
| ウ | Z(k) ← Y(k) | Z(m+k) ← X(k) |
| エ | Z(k) ← Y(k) | Z(n+k) ← X(k) |
令和1年7月修了試験 問7
次に示すユークリッドの互除法(方法1,方法2)で,正の整数a,bの最大公約数は,それぞれとnのどちらの変数に求まるか。ここで,m mod nは,mをnで割った余りを表す。
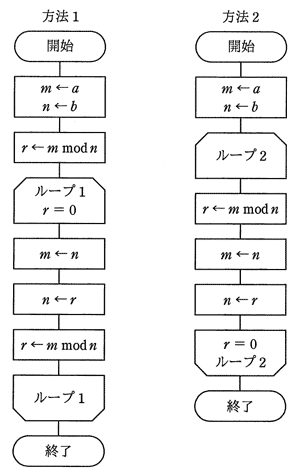

| 方法1 | 方法2 | |
| ア | m | m |
| イ | m | n |
| ウ | n | m |
| エ | n | n |
答え : ウ
分野 : テクノロジ系 › 基礎理論 › アルゴリズムとプログラミング › アルゴリズム
分野 : テクノロジ系 › 基礎理論 › アルゴリズムとプログラミング › アルゴリズム
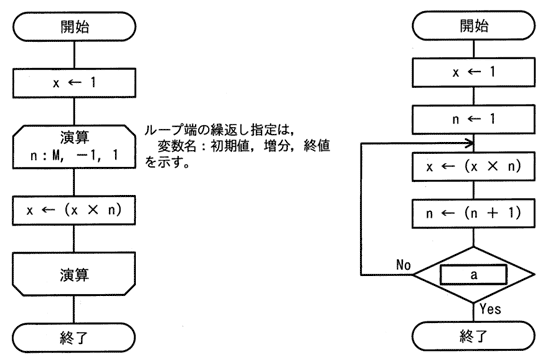
平成31年1月修了試験 問7
右の流れ図が左の流れ図と同じ動作をするために,a,bに入るYesとNoの組合せはどれか。
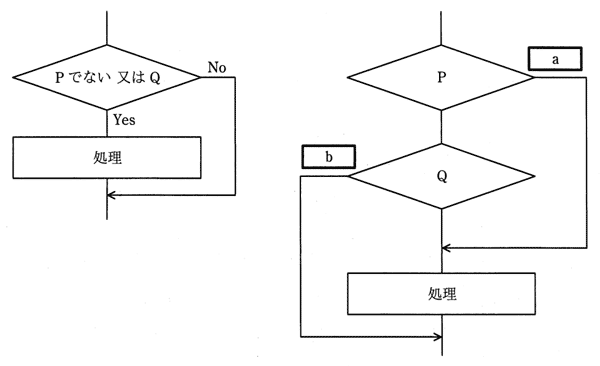

| a | b | |
| ア | No | No |
| イ | No | Yes |
| ウ | Yes | No |
| エ | Yes | Yes |
平成30年12月修了試験 問6
2分探索に関する記述のうち,適切なものはどれか。
| ア | 2分探索するデータ列は整列されている必要がある。 |
|---|---|
| イ | 2分探索は線形探索よりも常に速く探索できる。 |
| ウ | 2分探索は探索をデータ列の先頭から開始する。 |
| エ | n個のデータの2分探索に要する比較回数は,nlog2nに比例する。 |
平成30年秋期 問6
クイックソートの処理方法を説明したものはどれか。
| ア | 既に整列済みのデータ列の正しい位置に,データを追加する操作を繰り返していく方法である。 |
|---|---|
| イ | データ中の最小値を求め,次にそれを除いた部分の中から最小値を求める。この操作を繰り返していく方法である。 |
| ウ | 適当な基準値を選び,それよりも小さな値のグループと大きな値のグループにデータを分割する。同様にして,グループの中で基準値を選び,それぞれのグループを分割する。この操作を繰り返していく方法である。 |
| エ | 隣り合ったデータの比較と入替えを繰り返すことによって,小さな値のデータを次第に端の方に移していく方法である。 |
平成30年春期 問7
表探索におけるハッシュ法の特徴はどれか。
| ア | 2分木を用いる方法の一種である。 |
|---|---|
| イ | 格納場所の衝突が発生しない方法である。 |
| ウ | キーの関数値によって格納場所を決める。 |
| エ | 探索に要する時間は表全体の大きさにほぼ比例する。 |
平成29年7月修了試験 問6
昇順に整列済みの配列要素 A(1),A(2),...,A(n) から,A(m)=k となる配列要素A(m)の添字mを2分探索法によって見つける処理を図に示す。終了時点で m=0 である場合は,A(m)=k となる要素は存在しない。図中のaに入る式はどれか。ここで,“/” は,小数点以下を切り捨てる除算を表す。
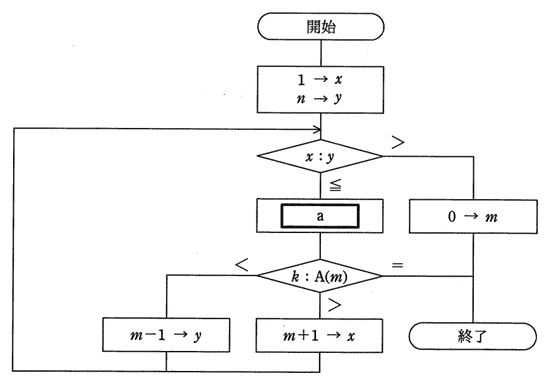

| ア | (x+y) → m |
|---|---|
| イ | (x+y)/2 → m |
| ウ | (x-y)/2 → m |
| エ | (y-x)/2 → m |
平成29年春期 問5
次の流れ図は,シフト演算と加算の繰返しによって2進整数の乗算を行う手順を表したものである。この流れ図中のa,bの組合せとして,適切なものはどれか。ここで,乗数と被乗数は符号なしの16ビットで表される。X,Y,Zは32ビットのレジスタであり,桁送りには論理シフトを用いる。最下位ビットを第0ビットと記す。
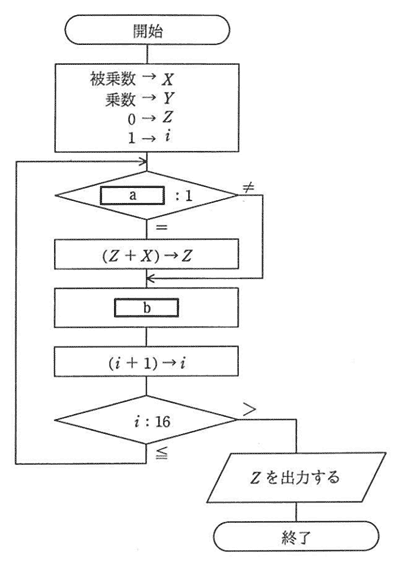

| a | b | |
| ア | Yの第0ビット | Xを1ビット左シフト,Yを1ビット右シフト |
| イ | Yの第0ビット | Xを1ビット右シフト,Yを1ビット左シフト |
| ウ | Yの第15ビット | Xを1ビット左シフト,Yを1ビット右シフト |
| エ | Yの第15ビット | Xを1ビット右シフト,Yを1ビット左シフト |
平成27年12月修了試験 問6
次の文章はあるソート(整列法)について述べたものである。そのソートはどれか。
“データの並びに対して基準となるある値を定めて,その値より小さいデータの並びが前半に,大きいデータが後半に並ぶように並べ替える。このようにして出来た前半の並び,及び後半の並びそれぞれに対して,再帰的に同じ操作を繰り返す。ここで,データの並びに対してその都度決める基準値は分割される。前半の並びと後半の並びの大きさが同じ程度の大きさになるように選ぶことが望ましい。”
“データの並びに対して基準となるある値を定めて,その値より小さいデータの並びが前半に,大きいデータが後半に並ぶように並べ替える。このようにして出来た前半の並び,及び後半の並びそれぞれに対して,再帰的に同じ操作を繰り返す。ここで,データの並びに対してその都度決める基準値は分割される。前半の並びと後半の並びの大きさが同じ程度の大きさになるように選ぶことが望ましい。”
| ア | 基数ソート |
|---|---|
| イ | クイックソート |
| ウ | バブルソート |
| エ | マージソート |
平成27年12月修了試験 問8
| ア | i=N |
|---|---|
| イ | i<N |
| ウ | i>N |
| エ | x>N |
平成27年春期 問6
| ア | logn |
|---|---|
| イ | n |
| ウ | n2 |
| エ | nlogn |
答え : ア
分野 : テクノロジ系 › 基礎理論 › アルゴリズムとプログラミング › アルゴリズム
分野 : テクノロジ系 › 基礎理論 › アルゴリズムとプログラミング › アルゴリズム
平成26年1月修了試験 問7
2,000個の相異なる要素が,キーの昇順に整列された表がある。外部から入力したキーによってこの表を2分探索して,該当するキーの要素を取り出す。該当するキーが必ず表中にあることが分かっているとき,キーの比較回数は最大何回か。
| ア | 9 |
|---|---|
| イ | 10 |
| ウ | 11 |
| エ | 12 |
答え : ウ
分野 : テクノロジ系 › 基礎理論 › アルゴリズムとプログラミング › アルゴリズム
分野 : テクノロジ系 › 基礎理論 › アルゴリズムとプログラミング › アルゴリズム
平成25年12月修了試験 問6
昇順に整列されたn個のデータが格納されている配列Aがある。流れ図は,2分探索法を用いて配列Aからデータを探し出す処理を表している。a,b に入る操作の適切な組合せはどれか。ここで,除算の結果は小数点以下が切り捨てられる。
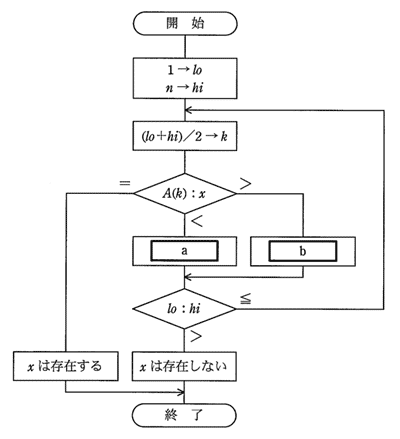

| a | b | |
| ア | k+1→hi | k-1→lo |
| イ | k-1→hi | k+1→lo |
| ウ | k+1→lo | k-1→hi |
| エ | k-1→lo | k+1→hi |
平成25年1月修了試験 問7
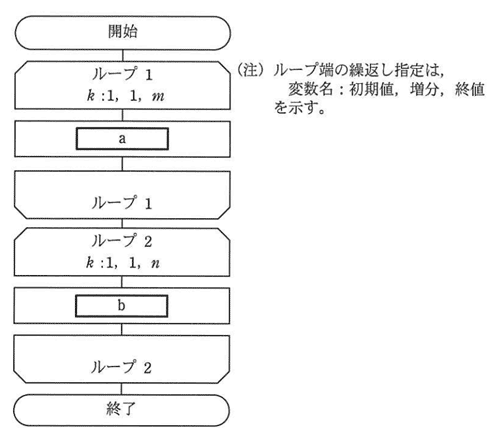
長さ m,n の文字列を格納した配列 X,Y がある。図は,長さの文字列の後ろに長さんの文字列を連結したものを配列Zに格納するアルゴリズムを表す流れ図である。図中の a,b に入れる処理として,適切なものはどれか。ここで,1文字が一つの配列要素に格納されるものとする。

| a | b | |
| ア | X(k) → Z(k) | Y(k) → Z(m+k) |
| イ | X(k) → Z(k) | Y(k) → Z(n+k) |
| ウ | Y(k) → Z(k) | X(k) → Z(m+k) |
| エ | Y(k) → Z(k) | X(k) → Z(n+k) |
平成24年秋期 問7
n!の値を,次の関数 F(n) によって計算する。乗算の回数を表す式はどれか。
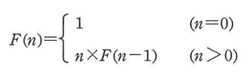
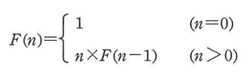
| ア | n-1 |
|---|---|
| イ | n |
| ウ | n2 |
| エ | n! |
答え : イ
分野 : テクノロジ系 › 基礎理論 › アルゴリズムとプログラミング › アルゴリズム
分野 : テクノロジ系 › 基礎理論 › アルゴリズムとプログラミング › アルゴリズム
平成24年7月修了試験 問7
次のような一連の代入文がある。
x+y → x
x-y → y
x-y → x
x,yの初期値をそれぞれA,Bとするとき,最後の代入文の実行が終了した時点におけるxとyの値の適切な組合せはどれか。
x+y → x
x-y → y
x-y → x
x,yの初期値をそれぞれA,Bとするとき,最後の代入文の実行が終了した時点におけるxとyの値の適切な組合せはどれか。
| x | y | |
| ア | A | B |
| イ | B | A |
| ウ | 2B | A-B |
| エ | A-B | A-B |
答え : イ
分野 : テクノロジ系 › 基礎理論 › アルゴリズムとプログラミング › アルゴリズム
分野 : テクノロジ系 › 基礎理論 › アルゴリズムとプログラミング › アルゴリズム
平成23年7月修了試験 問7
2分探索法に関する次の記述のうちで,適切なものはどれか。
| ア | データが昇順に並んでいるときだけ正しく探索できる。 |
|---|---|
| イ | データが昇順又は降順に並んでいるときだけ正しく探索できる。 |
| ウ | データが昇順又は降順に並んでいる方が効率よく探索できる。 |
| エ | データの個数が偶数のときだけ正しく探索できる。 |
答え : イ
分野 : テクノロジ系 › 基礎理論 › アルゴリズムとプログラミング › アルゴリズム
分野 : テクノロジ系 › 基礎理論 › アルゴリズムとプログラミング › アルゴリズム
平成23年6月修了試験 問7
| ア | |
|---|---|
| イ | |
| ウ | |
| エ |
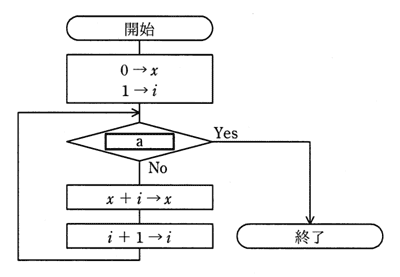
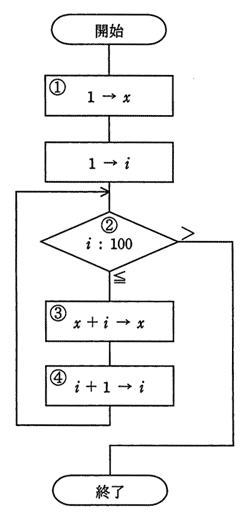
平成23年春期 問7
| ア | ①の処理を “0 → x” にする。 |
|---|---|
| イ | ②の条件判定を “i:99” にする。 |
| ウ | ③の処理を “x+i → i” にする。 |
| エ | ④の処理を “x+1 → x”にする。 |
答え : ア
分野 : テクノロジ系 › 基礎理論 › アルゴリズムとプログラミング › アルゴリズム
分野 : テクノロジ系 › 基礎理論 › アルゴリズムとプログラミング › アルゴリズム
平成22年1月修了試験 問6
あらかじめ整列された1000人の電話番号から,目的の電話番号を2分探索法を用いて探索するとき,最大およそ何回の比較が必要になるか。
| ア | 10 |
|---|---|
| イ | 46 |
| ウ | 500 |
| エ | 1000 |
答え : ア
分野 : テクノロジ系 › 基礎理論 › アルゴリズムとプログラミング › アルゴリズム
分野 : テクノロジ系 › 基礎理論 › アルゴリズムとプログラミング › アルゴリズム
平成21年12月修了試験 問7
6個の数値180,315,282,410,645,525を並べ替える。手順1~4は途中までの手順を示したものである。手順4まで終わったときの結果はどれか。
手順1 並びの左側から順に,数値の1の位の値によって0~9のグループに分ける。
手順2 次に0のグループの数値を左側から順に取り出して並べ,その右側に1のグループ,以下順に2~9のグループの数値を並べていく。
手順3 手順2で得られた数値の並びの左側から順に,数値の10の位によって0~9のグループに分ける。
手順4 手順2と同様に,0のグループの数値から順に並べる。
ここで,グループ内では,処理が行われた数値を左側から順に並べるものとする。
手順1 並びの左側から順に,数値の1の位の値によって0~9のグループに分ける。
手順2 次に0のグループの数値を左側から順に取り出して並べ,その右側に1のグループ,以下順に2~9のグループの数値を並べていく。
手順3 手順2で得られた数値の並びの左側から順に,数値の10の位によって0~9のグループに分ける。
手順4 手順2と同様に,0のグループの数値から順に並べる。
ここで,グループ内では,処理が行われた数値を左側から順に並べるものとする。
| ア | 180,282,315,410,525,645 |
|---|---|
| イ | 315,410,525,180,282,645 |
| ウ | 410,315,525,645,180,282 |
| エ | 645,525,410,315,282,180 |
答え : ウ
分野 : テクノロジ系 › 基礎理論 › アルゴリズムとプログラミング › アルゴリズム
分野 : テクノロジ系 › 基礎理論 › アルゴリズムとプログラミング › アルゴリズム
平成21年7月修了試験 問5
次の手順はシェルソートによる整列を示している。データ列7,2,8,3,1,9,4,5,6を手順(1)(4)に従って整列するとき,手順(3)を何回繰り返して完了するか。ここで,[ ] は小数点以下を切り捨てた結果を表す。
〔手順〕
(1)[データ数÷3]→Hとする。
(2)データ列を互いにH要素分だけ離れた要素の集まりからなる部分列とし,それぞれの部分列を,挿入法を用いて整列する。
(3)[H÷3]→Hとする。
(4)Hが0であればデータ列の整列は完了し,0でなければ(2)に戻る。
〔手順〕
(1)[データ数÷3]→Hとする。
(2)データ列を互いにH要素分だけ離れた要素の集まりからなる部分列とし,それぞれの部分列を,挿入法を用いて整列する。
(3)[H÷3]→Hとする。
(4)Hが0であればデータ列の整列は完了し,0でなければ(2)に戻る。
| ア | 2 |
|---|---|
| イ | 3 |
| ウ | 4 |
| エ | 5 |
答え : ア
分野 : テクノロジ系 › 基礎理論 › アルゴリズムとプログラミング › アルゴリズム
分野 : テクノロジ系 › 基礎理論 › アルゴリズムとプログラミング › アルゴリズム
平成21年7月修了試験 問6
ヒープソートの説明として,適切なものはどれか。
| ア | ある間隔おきに取り出した要素から成る部分列をそれぞれ整列し,更に間隔を詰めて同様の操作を行い,間隔が1になるまでこれを繰り返す。 |
|---|---|
| イ | 中間的な基準値を決めて,それよりも大きな値を集めた区分と,小さな値を集めた区分に要素を振り分ける。次に,それぞれの区分の中で同様な処理を繰り返す。 |
| ウ | 隣り合う要素を比較して,大小の順が逆であれば,それらの要素を入れ替えるという操作を繰り返す。 |
| エ | 未整列の部分を順序木にし,そこから最小値を取り出して整列済の部分に移す。この操作を繰り返して,未整列の部分を縮めていく。 |
答え : エ
分野 : テクノロジ系 › 基礎理論 › アルゴリズムとプログラミング › アルゴリズム
分野 : テクノロジ系 › 基礎理論 › アルゴリズムとプログラミング › アルゴリズム