M/M/1モデル【M/M/1待ち行列】

概要

M/M/1モデル（M/M/1待ち行列）とは、最も基本的な待ち行列のモデルの一つで、一つの窓口にランダムにやってくる利用者が、各々ランダムな時間だけ窓口を占有するという状態をモデル化したもの。

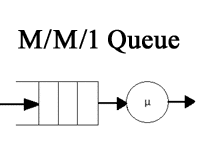
M/M/1モデルでは「窓口に人がやってくる時間間隔はポアソン分布に従ってランダムである」「各々が窓口で用を足す時間の長さは指数分布に従ってランダムである」「窓口の数は一つ」の3つの条件を満たす待ち行列について分析する。

単位時間あたりに窓口に来る人数を処理できる人数で割ったものを利用率という。M/M/1モデルにおける平均の待ち時間は利用率を用いて、利用率/（1-利用率）×平均サービス時間という式で表されることが知られている。

M/M/1モデルはレジや券売機、ATMに利用者が並んでいる様子を表す数学的なモデルとしてよく知られるが、ITの分野でも、一台のサーバに次々にクライアントが要求を送信し、サーバがこれを処理して応答するといったシステムの挙動を分析するのに有用である。

「M/M/1」の表記は「ケンドールの記号」と呼ばれる表記法の一つで、待ち行列の特徴を表している。先頭から順に、到着の過程、処理時間の分布、窓口の数を表した略号である。到着がポアソン分布に従うマルコフ過程、処理時間は指数分布に従うマルコフ過程であるため、いずれも “Memoryless” （無記憶）あるいは “Markovian” の頭文字を取って「M」となる。窓口は一つのため「1」で、順に繋げると「M/M/1」となる。

(2023.2.24更新)