読み方：アルファベータほう

概要

αβ法（アルファベータ法）とは、ゲーム理論で最適な手番を探索する手法であるミニマックス法を改良したもの。それまでに発見した値に基づいて探索する必要のない枝を切り捨てることで探索を高速化する。

ミニマックス法とは

ミニマックス法では、二者が交互に自分の行動を選択するようなゲームで、自分の手番では自分の利得が最も大きくなるように、相手の手番では自分の利得が最も小さくなるような選択肢を選んだとき、自分の利得が最も大きくなる選択肢がどれになるか探索する。

ゲームの展開は手番ごとに選択肢の数だけ枝分かれしていく木構造で表すことができ、これを「ゲーム木」という。頂点は自分の手番、2段目は相手の手番、3段目は自分の手番…というように、自分と相手の手番が交互に現れる。

何手か先までのゲーム木を構築し、末端には頂点からその経路をたどったときの結果（自分の利得）を書き入れる。末端の値から順に木を遡り、自分の手番では自分の利得が最大（max）になる選択肢を、相手の手番では自分の利得が最小（mini）になる手番を打つと仮定し、各手番の打ち手を決定していく。

αβ法とは

ミニマックス法ではすべての選択肢を頂点までたどるが、αβ法では探索の途中で明らかに可能性のない枝を発見して、たどらないようにすることで計算時間を短縮する。これを「枝刈り」という。

具体的には、現在までの探索で発見した値の中で、自分の手番における利得の最大値をα値、相手の手番における自分の利得の最小値をβ値として記録する。探索の最初にはどちらの値も空だが、一つの枝をたどると、その時点での暫定的な最大値α、最小値βが得られる。

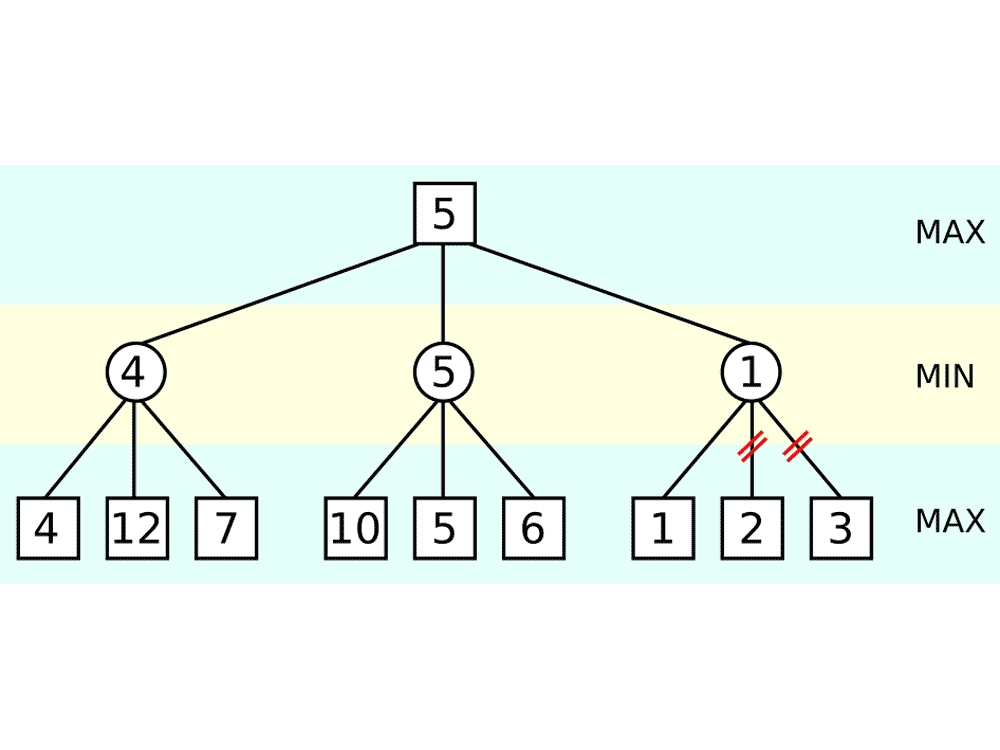
次の枝を探索する際、自分の手番でαより小さい値しかない枝は探索する必要がないため省略する（αカット）。同じように、相手の手番でβより大きい値しかない枝は必要ないため省略する（βカット）。途中でαより大きい値が見つかったら更新し、βより小さい値が見つかったらやはり更新する。

探索が進めば進むほど、すでに発見したα値、β値により探索が不要な枝が増えていく。α値とβ値自体も更新を繰り返して最終的な解に近づいていくため、終盤には加速度的にαカットあるいはβカットされる枝が増えることになる。