読み方 ： にぶんたんさくぎ

概要

二分探索木（binary search tree）とは、データ構造の一つである二分木(バイナリツリー)のうち、各ノードの値よりも左の子ノードの値の方が小さく、右の子ノードの値の方が大きくなるように構築したもの。データの探索に適したデータ構造である。

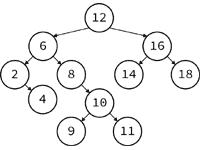
解説 木構造はグラフ構造のうち要素に親子関係があり、親が複数の子を持つことができるようなものを意味し、根ノード（root node）を頂点として階層的に枝分かれしていく構造となる。どの親ノードも子ノードを一つか二つしか持たないという制限を課されたものを「二分木」（binary tree/2分木）という。

二分探索木は二分木を構築する際に、どのノードも「左の子孫の値≦自らの値≦右の子孫の値」という条件を満たすように値を挿入していく。根ノードから出発して、挿入値が現在のノードより小さければ左の子、大きければ右の子ノードに移動していき、末端のノード（葉ノード）に達したら次に移動すべき場所に新たなノードを作成して値を格納する。N個の値の挿入には O（log N） の計算量がかかる。

格納された値を探索する際には、根ノードから出発して、各ノードの値が探索している値より大きければ左の子に、小さければ右の子ノードに移動していき、葉ノードまでたどる間に値が見つかれば探索は打ち切り、葉ノードに至っても値が見つからなければ「目的の値は存在しない」という結論になる。ノードがN個の木の探索には O（log N） の計算量がかかる。

このような探索法を「二分探索」（バイナリサーチ/二分探索法）という。根から葉までの深さ（高さ）の数だけ値を調べればよく、値を単純に端から順番に調べるより効率的に探索できる。なお、木にデータを追加する際に親と同じ値を左右どちらのノードに入れるかは任意だが、毎回異なることがないようあらかじめ決めておく。

平衡二分探索木 (self-balancing binary search tree)

二分探索木のうち、根ノードから子を持たない末端の葉ノードまでの深さ（高さ）がなるべく均等になるように構築されたものを「平衡二分探索木」という。

二分探索木で値を探索するには、根ノードから出発して、各ノードの値が探索している値より大きければ左の子に、小さければ右の子に移っていくが、枝によって深さがまちまちだと探索終了までの比較回数にばらつきが出る。

根から葉までの距離がなるべく均等な方が比較回数が揃って平均的に効率よく探索できるため、平衡二分探索木では値の挿入や削除の際に高さが均等になるような処理を行う。代償として、木の構築の際には平衡を考慮しない単純な二分探索木より時間がかかる。