基本情報技術者(科目A)過去問集 - 応用数学
令和7年7月修了試験 問1
次の例に示すように,関数 f(x) はx以下で最大の整数を表す。
f(1.0) = 1
f(0.9) = 0
f(-0.4) = -1
小数点以下1桁の小数 -0.9,-0.8,…,-0.1,0.0,0.1,…,0.8,0.9 からxを等確率で選ぶとき,f(x+0.5) の期待値(平均値)は幾らか。
f(1.0) = 1
f(0.9) = 0
f(-0.4) = -1
小数点以下1桁の小数 -0.9,-0.8,…,-0.1,0.0,0.1,…,0.8,0.9 からxを等確率で選ぶとき,f(x+0.5) の期待値(平均値)は幾らか。
| ア | |
|---|---|
| イ | |
| ウ | |
| エ |
令和7年7月修了試験 問2
5本のくじがあり,そのうち2本が当たりである。同時にくじを2本引いたとき,2本とも当たりである確率は幾らか。
| ア | |
|---|---|
| イ | |
| ウ | |
| エ |
令和7年7月修了試験 問4
通信回線を使用したデータ伝送システムにM/M/1の待ち行列モデルを適用すると,平均回線待ち時間,平均伝送時間,回線利用率の関係は,次の式で表すことができる。
回線利用率が0から徐々に増加していく場合,平均回線待ち時間が平均伝送時間よりも最初に長くなるのは,回線利用率が幾つを超えたときか。
回線利用率が0から徐々に増加していく場合,平均回線待ち時間が平均伝送時間よりも最初に長くなるのは,回線利用率が幾つを超えたときか。
| ア | 0.4 |
|---|---|
| イ | 0.5 |
| ウ | 0.6 |
| エ | 0.7 |
令和7年7月修了試験 問6
次の数式は,ある細菌の第n世代の個数f(n)が1世代後にどのように変化するかを表現したものである。この漸化式の解釈として,1世代後の細菌の個数が,第n世代と比較してどのようになるかを適切に説明しているものはどれか。
f(n+1) + 0.2 × f(n) = 2 × f(n)
f(n+1) + 0.2 × f(n) = 2 × f(n)
| ア | 1世代後の個数は,第n世代の個数の1.8倍に増える。 |
|---|---|
| イ | 1世代後の個数は,第n世代の個数の2.2倍に増える。 |
| ウ | 1世代後の個数は,第n世代の個数の2倍になり,更に増殖後の20%が増える。 |
| エ | 1世代後の個数は,第n世代の個数の2倍になるが,増殖後の20%が死ぬ。 |
令和7年6月修了試験 問2
標準偏差に関する記述のうち,適切なものはどれか。
| ア | すべてのデータに定数aを加えたものの標準偏差は,元の標準偏差にaを加えたものになる。 |
|---|---|
| イ | すべてのデータに定数aを加えたものの標準偏差は,元の標準偏差のa倍になる。 |
| ウ | すべてのデータを2倍したものの標準偏差は,元の標準偏差の1/2となる。 |
| エ | すべてのデータを2倍したものの標準偏差は,元の標準偏差の2倍になる。 |
令和7年公開問題 問2
浮動小数点形式で表現された数値の演算結果における丸め誤差の説明はどれか。
| ア | 演算結果がコンピュータの扱える最大値を超えることによって生じる誤差である。 |
|---|---|
| イ | 数表現のけた数に限度があるので,最下位けたより小さい部分について四捨五入や切上げ,切捨てを行うことによって生じる誤差である。 |
| ウ | 乗除算において,指数部が小さい方の数値の仮数部の下位部分が失われることによって生じる誤差である。 |
| エ | 絶対値がほぼ等しい数値の加減算において,上位の有効数字が失われることによって生じる誤差である。 |
答え : イ
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 応用数学
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 応用数学
令和7年1月修了試験 問2
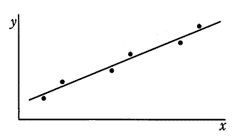
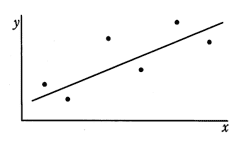
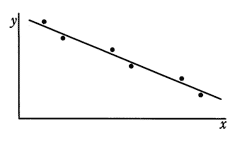
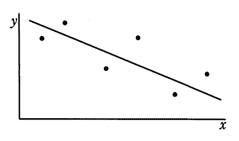
相関係数に関する記述のうち,適切なものはどれか。
| ア | 全ての標本点が正の傾きをもつ直線上にあるときは,相関係数が+1になる。 |
|---|---|
| イ | 変量間の関係が線形のときは,相関係数が0になる。 |
| ウ | 変量間の関係が非線形のときは,相関係数が負になる。 |
| エ | 無相関のときは,相関係数が-1になる。 |
令和6年7月修了試験 問2
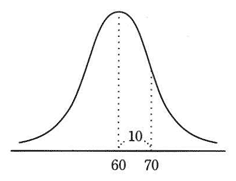
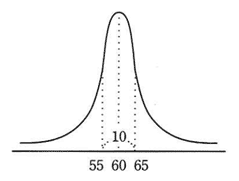
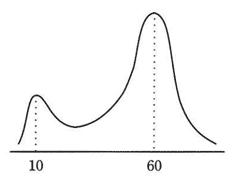
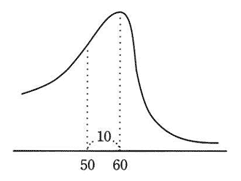
正規分布の説明として,適切なものはどれか。
| ア | 故障確率に用いられ,バスタブのような形状をした連続確率分布のこと |
|---|---|
| イ | 全ての事象の起こる確率が等しい現象を表す確率分布のこと |
| ウ | 平均値を中心とする左右対称で釣鐘状の連続確率分布のこと |
| エ | 離散的に発生し,発生確率は一定である離散確率分布のこと |
令和6年7月修了試験 問4
コンピュータで連立一次方程式の解を求めるのに,式に含まれる未知数の個数の3乗に比例する計算時間が掛かるとする。あるコンピュータで100元連立一次方程式の解を求めるのに2秒掛かったとすると,その4倍の演算速度をもつコンピュータで1,000元連立一次方程式の解を求めるときの計算時間は何秒か。
| ア | 5 |
|---|---|
| イ | 50 |
| ウ | 500 |
| エ | 5,000 |
令和6年6月修了試験 問4
多数のクライアントが,LANに接続された1台のプリンタを共同利用するときの印刷要求から印刷完了までの所要時間を,待ち行列理論を適用して見積もる場合について考える。プリンタの運用方法や利用状況に関する記述のうち,M/M/1の待ち行列モデルの条件に反しないものはどれか。
| ア | 一部のクライアントは,プリンタの空き具合を見ながら印刷要求をする。 |
|---|---|
| イ | 印刷の緊急性や印刷量の多少にかかわらず,先着順に印刷する。 |
| ウ | 印刷待ち文書の総量がプリンタのバッファサイズを超えるときは,一時的に受付を中断する。 |
| エ | 一つの印刷要求から印刷完了までの所要時間は,印刷の準備に要する一定時間と,印刷量に比例する時間の合計である。 |
令和5年7月修了試験 問2
正三角形の内部の点から,各辺に下ろした垂線の長さの和は一定である(図1参照)。三角グラフは,この性質を利用して,三つの辺に対応させた要素の割合を各辺への垂線の長さとして表したグラフである。図2の三角グラフは,3種類のソフトについて,A~D の4人の使用率を図示したものである。正しい解釈はどれか。
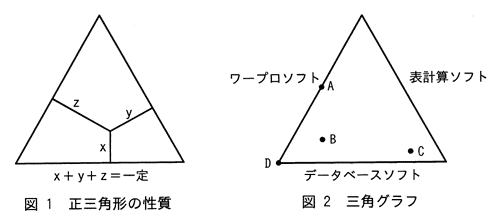

| ア | Aさんは,ワープロソフトだけを使用している。 |
|---|---|
| イ | Bさんは,ほかのソフトに比べて表計算ソフトの使用率が高い。 |
| ウ | Cさんは,データベースソフト,表計算ソフト,ワープロソフトの順に使用率が高い。 |
| エ | Dさんは,表計算ソフトを使用していない。 |
令和4年12月修了試験 問3
表は,ある地方の天気の移り変わりを示したものである。例えば,晴れの翌日の天気は,40%の確率で晴れ,40%の確率で曇り,20%の確率で雨であることを表している。天気の移り変わりが単純マルコフ過程であると考えたとき,雨の2日後が晴れである確率は何%か。
単位 %
単位 %
| 翌日晴れ | 翌日曇り | 翌日雨 | |
| 晴れ | 40 | 40 | 20 |
| 曇り | 30 | 40 | 30 |
| 雨 | 30 | 50 | 20 |
| ア | 15 |
|---|---|
| イ | 27 |
| ウ | 30 |
| エ | 33 |
令和4年7月修了試験 問2
隣接行列Aで表されるグラフはどれか。ここで,隣接行列とは,n個の節点から成るグラフの節点ViとVjを結ぶ枝が存在するときは第i行第j列と第j行第i列の要素が1となり,存在しないときは0となるn行n列の行列である。
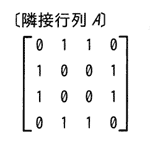

| ア | 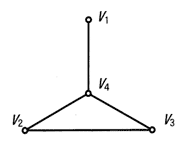 |
|---|---|
| イ | 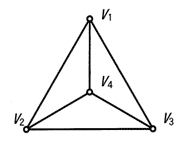 |
| ウ | 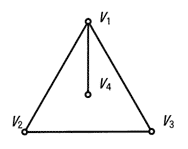 |
| エ | 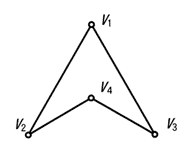 |
令和4年6月修了試験 問4
ノードとノードの間のエッジの有無を,隣接行列を用いて表す。ある無向グラフの隣接行列が次の場合,グラフで表現したものはどれか。ここで,ノードを隣接行列の行と列に対応させて,ノード間にエッジが存在する場合は1で,エッジが存在しない場合は0で示す。


| ア | 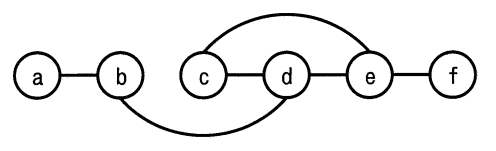 |
|---|---|
| イ | 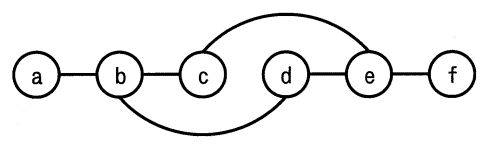 |
| ウ | 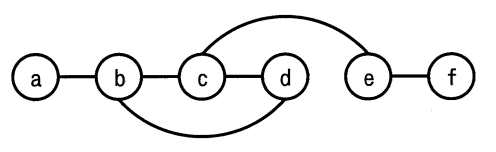 |
| エ | 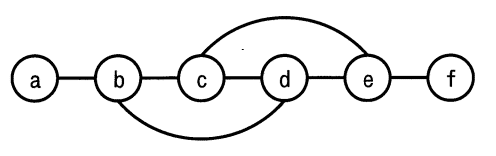 |
令和3年12月修了試験 問3
さいころを投げて,出た目に応じて得点するゲームを行う。出た目が 1~4 の場合はその目を得点とし,目が5,6の場合は得点はない。さいころを1回投げたときの得点の期待値は幾らか。
| ア | |
|---|---|
| イ | |
| ウ | |
| エ |
令和3年12月修了試験 問4
連立一次方程式
から,xの項の係数,yの項の係数,及び定数項だけを取り出した表(行列)を作り,基本操作(1)~(3)のいずれかを順次施すことによって,解
が得られた。表(行列)が次のように左から右に推移する場合,同じ種類の基本操作が施された箇所の組合せはどれか。
〔基本操作〕
(1)ある行に0でない数を掛ける。
(2)ある行と他の行を入れ替える。
(3)ある行に他の行の定数倍を加える。
〔表(行列)の推移〕

から,xの項の係数,yの項の係数,及び定数項だけを取り出した表(行列)を作り,基本操作(1)~(3)のいずれかを順次施すことによって,解
が得られた。表(行列)が次のように左から右に推移する場合,同じ種類の基本操作が施された箇所の組合せはどれか。
〔基本操作〕
(1)ある行に0でない数を掛ける。
(2)ある行と他の行を入れ替える。
(3)ある行に他の行の定数倍を加える。
〔表(行列)の推移〕

| ア | aとb |
|---|---|
| イ | aとc |
| ウ | bとc |
| エ | bとd |
答え : イ
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 応用数学
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 応用数学
令和2年12月修了試験 問4
Random(n) は,0以上n未満の整数を一様な確率で返す関数である。整数型の変数A,B及びCに対して次の一連の手続を実行したとき,Cの値が0になる確率はどれか。
A = Random(10)
B = Random(10)
C = A-B
A = Random(10)
B = Random(10)
C = A-B
| ア | |
|---|---|
| イ | |
| ウ | |
| エ |
令和2年7月修了試験 問3
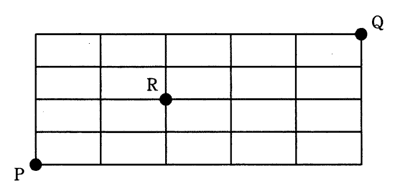
図の線上を,点Pから点Rを通って,点Qに至る最短経路は何通りあるか。

| ア | 16 |
|---|---|
| イ | 24 |
| ウ | 32 |
| エ | 60 |
令和2年6月修了試験 問3
(1+α)n の計算を,1+n×α で近似計算ができる条件として,適切なものはどれか。
| ア | |α|が1に比べて非常に小さい。 |
|---|---|
| イ | |α|がnに比べて非常に大きい。 |
| ウ | |α÷n|が1よりも大きい。 |
| エ | |n×α|が1よりも大きい。 |
令和2年1月修了試験 問3
浮動小数点形式で表現された数値の演算結果における丸め誤差の説明はどれか。
| ア | 演算結果がコンピュータの扱える最大値を超えることによって生じる誤差である。 |
|---|---|
| イ | 数表現のけた数に限度があるので,最下位けたより小さい部分について四捨五入や切上げ,切捨てを行うことによって生じる誤差である。 |
| ウ | 乗除算において,指数部が小さい方の数値の仮数部の下位部分が失われることによって生じる誤差である。 |
| エ | 絶対値がほぼ等しい数値の加減算において,上位の有効数字が失われることによって生じる誤差である。 |
平成29年1月修了試験 問3
関数 eq(X,Y)は,引数XとYの値が等しければ1を返し,異なれば0を返す。整数A,B,Cについて,eq(eq(A,B),eq(B,C))を呼び出したとき,1が返ってくるための必要十分条件はどれか。
| ア | (A=BかつB=C)又は(A≠BかつB≠C) |
|---|---|
| イ | (A=BかつB=C)又は(A≠B又はB≠C) |
| ウ | (A=BかつB=C)又はA=C |
| エ | (A=B又はB=C)又はA=C |
平成27年1月修了試験 問2
| ア | A∧B |
|---|---|
| イ | A∧B |
| ウ | A∨B |
| エ | A∨B |
平成23年春期 問2
三つの実数 X~Z とそれぞれの近似値が次の場合,相対誤差の小さい順に並べたものはどれか。
| 真の値 | 近似値 | |
| X | 1.02 | 1 |
| Y | 1.97 | 2 |
| Z | 5.05 | 5 |
| ア | X,Y,Z |
|---|---|
| イ | Y,Z,X |
| ウ | Z,X,Y |
| エ | Z,Y,X |
答え : エ
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 応用数学
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 応用数学
平成22年12月修了試験 問3
白玉4個,赤玉5個が入っている袋から玉を1個取り出し,それを元に戻さないで続けてもう1個取り出すとき,2個とも赤である確率は幾らか。
| ア | |
|---|---|
| イ | |
| ウ | |
| エ |
平成22年7月修了試験 問3
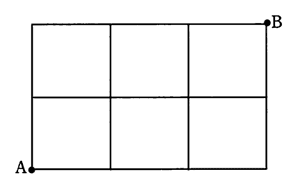
図のA地点から,線上をたどってB地点に到達するための最短経路は,何通りあるか。ここで,縦1区画の長さはすべて等しく,横1区画の長さもすべて等しい。

| ア | 7 |
|---|---|
| イ | 9 |
| ウ | 10 |
| エ | 12 |
答え : ウ
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 応用数学
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 応用数学
平成21年秋期 問1
| ア | |
|---|---|
| イ | |
| ウ | |
| エ |
答え : エ
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 応用数学
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 応用数学
平成21年7月修了試験 問3
ある工場で製造している部品の長さの誤差は,平均0mm,標準偏差0.5mmの正規分布に従っている。誤差の許容範囲が±1mmのとき,不良品の発生率は何%になるか。標準正規分布表を用いて最も近い値を選べ。
標準正規分布表
標準正規分布表
| 確率変数 | 分布関数値 | 確率密度関数値 |
| 0.00 | 0.5000 | 0.3938 |
| 0.50 | 0.6915 | 0.3521 |
| 1.00 | 0.8413 | 0.2420 |
| 1.50 | 0.9332 | 0.1296 |
| 2.00 | 0.9773 | 0.0540 |
| 2.50 | 0.9938 | 0.0175 |
| 3.00 | 0.9987 | 0.0044 |
| 3.50 | 0.9998 | 0.0009 |
| ア | 2.3 |
|---|---|
| イ | 4.5 |
| ウ | 5.4 |
| エ | 15.9 |
答え : イ
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 応用数学
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 応用数学
平成21年7月修了試験 問4
1~6の目をもつさいころ二つを同時に振り,その目の和を求める。これを十分な回数実行したときの和の分布はどれか。
| ア | 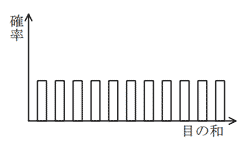 |
|---|---|
| イ | 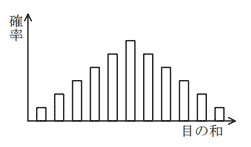 |
| ウ | 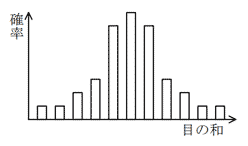 |
| エ | 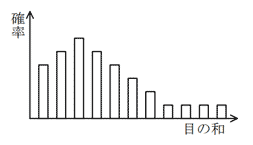 |
答え : イ
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 応用数学
分野 : テクノロジ系 › 基礎理論 › 基礎理論 › 応用数学