読み方：せんけいかいき

線形回帰【linear regression】

概要

線形回帰（linear regression）とは、何かの結果を表す数値の系列があるとき、原因と考えられる数値の系列を用いて直線的な比例関係として表すこと。

調査などで得られた様々な数値の組み合わせのうち、着目している数値（目的変数/従属変数）が、他の数値（説明変数）から一次式で算出される線形の関係にある状態を指す。説明変数が一つの場合を「線形単回帰」、複数の場合を「線形重回帰」という。

説明変数を $x$ 、目的変数を $y$ とする線形単回帰の場合、2つの変数の関係は $y = ax + b$ という一次関数で近似される。任意の $x$ の値をこの式に代入すれば、未知の $y$ の値を予測・推測できるようになる。

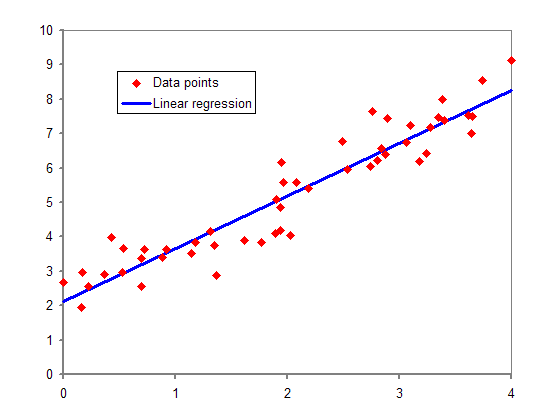
横軸を説明変数、縦軸を目的変数とする散布図で表すと、線形回帰は分布の様子を直線で近似したものと考えることができる。 $y = ax + b$ の $a$ は直線の傾きを、 $b$ はy切片を表している。直線の取り方には様々な可能性が考えられるが、実際のデータを表す各点との距離がなるべく小さくなることが望ましく、「最小二乗法」などの計算法で係数 $a$ と $b$ の値を決定する。

説明変数 $x_{i}$ において、実測された目的変数は $y_{i}$ 、回帰式から求めた予測値は $a x_{i} + b$ となる。両者の差である $y_{i} - a x_{i} - b$ を2乗し、各点について合計したものを「残差平方和」という。これが最小になるときの $a$ および $b$ を算出すると、 $x$ と $y$ の平均 $\bar{x}$ と $\bar{y}$ 、標準偏差 $S_{x}$ と $S_{y}$ 、相関係数 $r$ を用いて、 $b = r \frac{S_{y}}{S_{x}}$ 、 $a = \bar{y} - b \bar{x}$ として表すことができる。