読み方 : レルーかんすう
ReLU関数【Rectified Linear Unit】ランプ関数/ramp function
概要
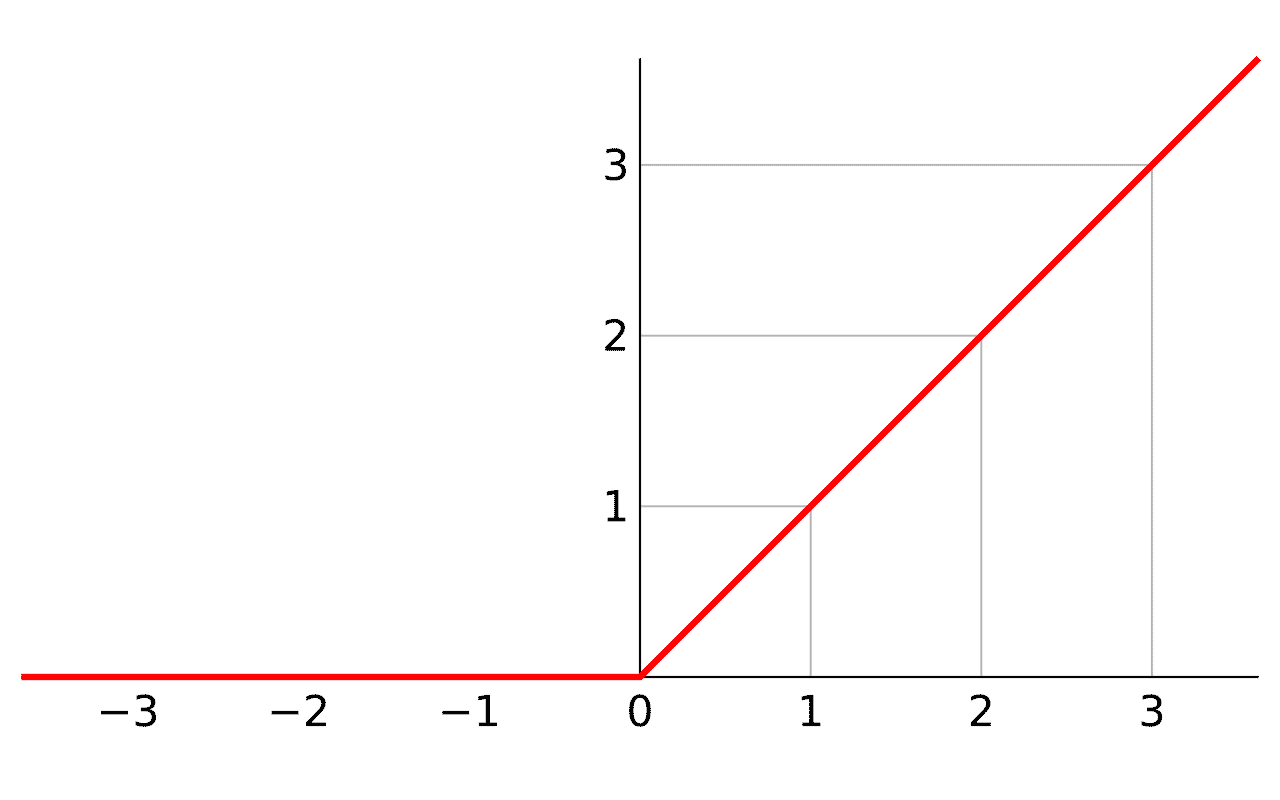
ReLU関数とは、入力が0以下なら0を返し、0より大きければその値をそのまま返す関数。ニューラルネットワークの活性化関数として用いられる。計算が単純で学習を高速化でき、階層が深くなっても勾配消失が起こりにくいという特徴がある。
ニューラルネットワークで各ノードが上位層のノードから受け取った値の和を非線形変換するために用いる「活性化関数」の一つである。研究初期に用いられたシグモイド関数やtanh関数の課題であった、出力層から誤差を遡って伝達していくと微分値の掛け算が繰り返されて初期層側で誤差が0に近くなってしまう「勾配消失」が起こりにくい。
数式としては と表される。入力が正の領域ではグラフが の傾き45度の右上がりの直線となり、線形的に値が増加する。負の領域では常に0となる。極めて単純な形式であるため、ネットワークに非線形性を導入しつつも計算負荷を抑えることができる。
多数の層を重ねても学習が進みやすいとされ、畳み込みニューラルネットワーク(CNN)をはじめとする多くのモデルで標準的に採用されている。特に勾配計算の容易さが学習効率の向上に寄与し、大規模データセットを扱う際の学習時間の短縮、単位時間あたりの学習量の増大に繋がる点が好まれている。
一方で、入力が負の領域に入ると勾配が0になり、特定のノードの重みが更新されなくなる「死んだReLU問題」(dying ReLU)と呼ばれる現象が生じることがある。この点を改善するため、負の領域でもわずかに傾きを維持するLeaky ReLU関数などの派生手法も考案されている。ReLU自体は依然として簡潔で扱いやすい活性化関数として広く利用されている。
(2025.11.27更新)