読み方：あんてん

鞍点【saddle point】

概要

鞍点とは、変数が2つ以上ある多変数関数のグラフで、ある方向では極大値だが、別のある方向では極小値となる特殊な点のこと。局所的な最大値や最小値とは異なり、関数の勾配がゼロであっても安定性を持たない。

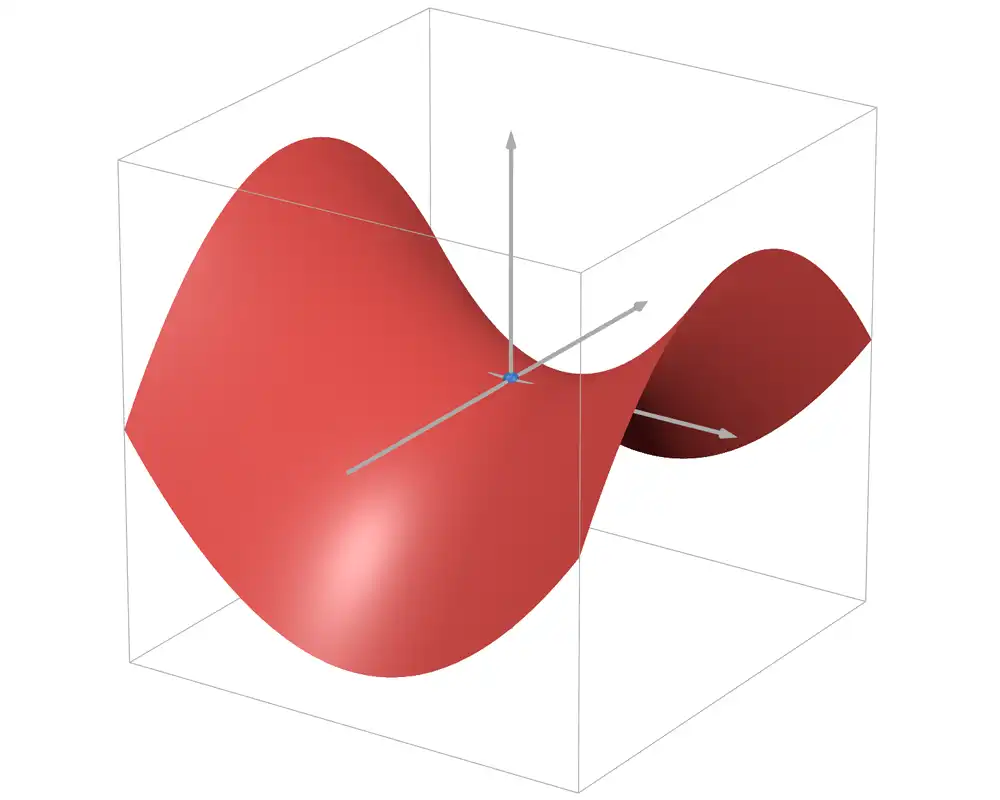
鞍点は二次元以上の関数解析で用いられる概念である。関数の形状を山と谷で例えると、鞍点は峠や馬の鞍のように前後方向で谷、左右方向で山となる位置に相当する。数学的には、点における勾配ベクトルがゼロとなり、ヘッセ行列（二次微分の行列）の固有値が正と負の両方を持つ場合に鞍点であると判定される。

統計解析や数理最適化では、目的関数を最適化する際に鞍点が現れることがあり、特に多数の変数を扱う高次元空間では、変数の組み合わせによって多数の鞍点が出現することがある。勾配降下法などの反復最適化手法では、鞍点付近で勾配が小さくなるため、学習や探索が停滞する場合がある。

鞍点は極値ではないため、最終的な解として採用されることは通常なく、最適解を探索する上での障害となることが多い。関数の形状や勾配の解析において、鞍点の存在を理解することは収束挙動の予測やアルゴリズム設計において重要である。

深層学習（ディープラーニング）では誤差関数の空間は非常に高次元であり、初期のアルゴリズムは多数の鞍点に阻まれて最適化が停滞する問題に悩まされたが、現在用いられている「Adam」や「RMSprop」のような適応的な学習率を持つ手法は、鞍点の周辺でも停滞することなく最小値に向かって抜け出すよう工夫されている。

(2025.12.3更新)