読み方：にこうぶんぷ

概要

二項分布（binomial distribution）とは、2つの事象のどちらかになる試行を何度も繰り返したとき、片方の事象が出る回数が従う確率分布のこと。例えば、コインを10回投げたとき、表が出る回数とその確率が該当する。

コインを投げたときの表裏のように2つの結果のいずれかが確率的に生じる試行を「ベルヌーイ試行」という。コインの場合は表が出る確率が0.5、裏が0.5だが、一般には均等である必要はなく、片方が出る確率をpとするともう片方が出る確率は1-pとなる。

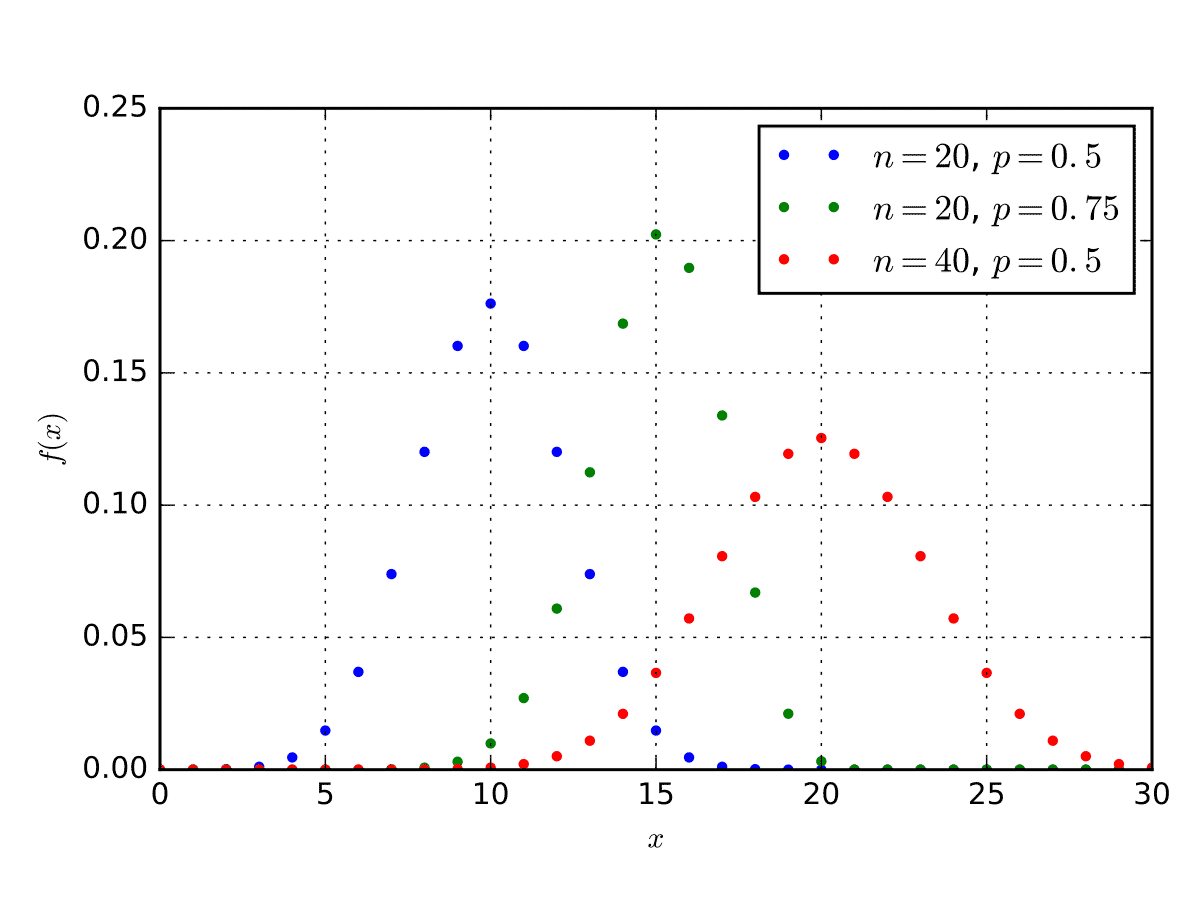
このような試行をn回行ったとき、確率pで生じる片方の事象（ベルヌーイ試行では便宜上「成功」という）が出る回数Xが何回になるかは確率的に決まり、回数と確率の対応はnとpによって定まる法則性を持っている。このXの確率分布のことを二項分布という。

n回の試行を行って、成功（確率p）がk回、失敗（確率1-p）がn-k回の状態になる確率は p^k（1-p）^n-k となる。一方、この状態になる場合の数は、n個の結果にk個の成功を当てはめる組み合わせの数であるため、 nCk となる。両者の積が、Xがkとなる確率を表している。

統計解析では、ある条件に当てはまる個体の割合がpである母集団から、n個の標本を無作為に取り出したときに条件に当てはまる標本の数Xの確率分布が、nとpで決まる二項分布となる。この性質を利用して統計的な有意性を判断する検定手法を「二項検定」という。