読み方 ： きょくしょさいてきかい

概要

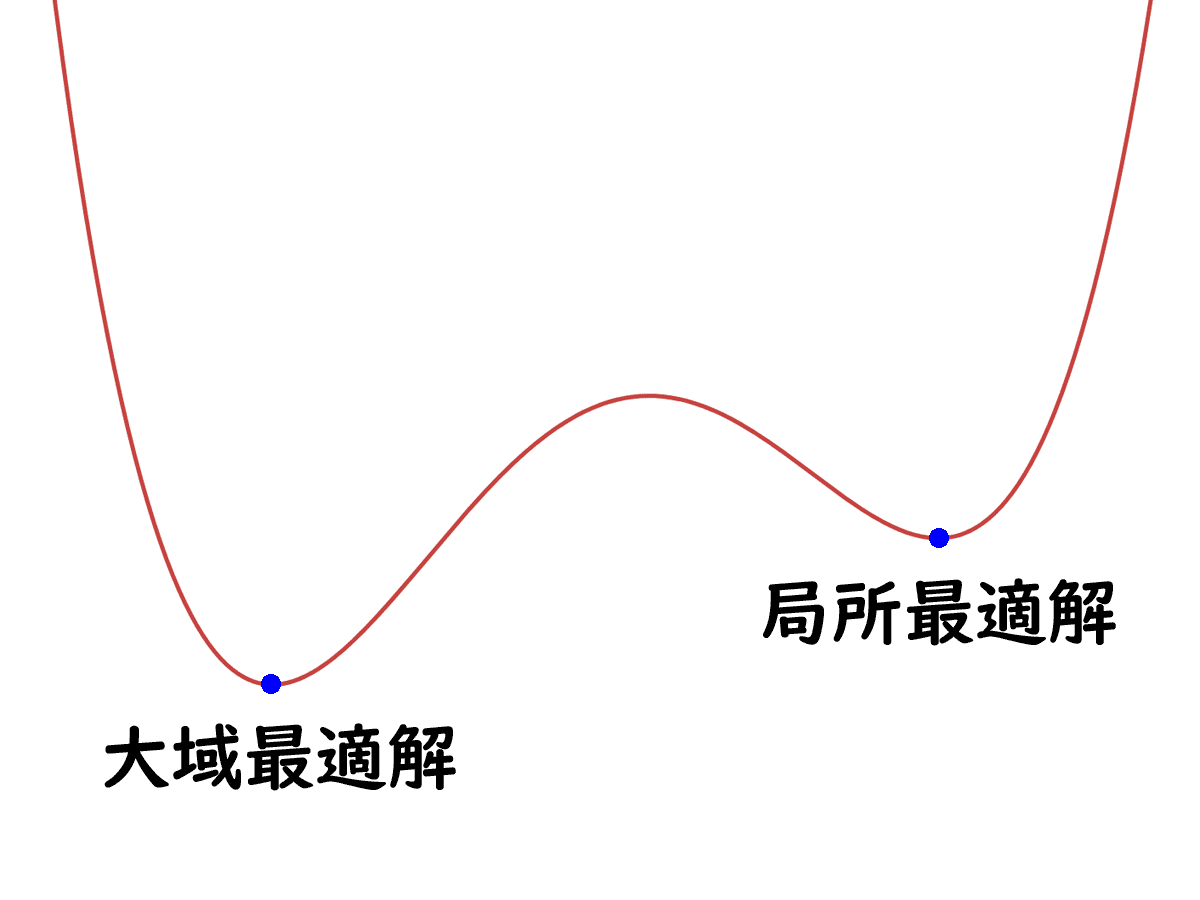
関数のグラフを描いたときに山の頂点や谷底になっている箇所で、周囲に比べて最も高い、あるいは低い状態になっているが、関数の定義域全体を調べたときに最も高い・低い箇所である大域最適解になっているとは限らない。

機械学習では多変数で非線形の複雑な関数の最適化を行うため、勾配降下法など数値的な解法を用いることがある。これは、ある地点から始めて、関数の値が下がっていく方向に向かって少しずつ移動していく手法だが、底に到達すると勾配がゼロになり、そこが大域最適解でなくても探索を停止してしまう。

局所最適解が存在すると、モデルの訓練結果が初期値に強く依存するという問題が生じる。パラメータの初期設定が異なると、勾配降下法が異なる「谷」に誘導され、それぞれ異なる局所最適解に収束し、異なる結果となるためである。局所最適解に留まらずに大域最適解を探索させるため、モーメンタムやAdamなどの学習率に「慣性」を加える最適化手法や、訓練中にあえてノイズを加える手法などが考案されている。

この記事の著者 ： (株)インセプト IT用語辞典 e-Words 編集部
1997年8月より「IT用語辞典 e-Words」を執筆・編集しています。累計公開記事数は1万ページ以上、累計サイト訪問者数は1億人以上です。学術論文や官公庁の資料などへも多数の記事が引用・参照されています。