ITパスポート過去問集 - 離散数学

令和6年問83

1から6までの六つの目をもつサイコロを3回投げたとき，1回も1の目が出ない確率は幾らか。

ア	$\frac{1}{216}$
イ	$\frac{5}{72}$
ウ	$\frac{91}{216}$
エ	$\frac{125}{216}$

答え：エ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
解説：
サイコロを1回投げたとき、1以外が出る確率は

\frac{5}{6}

です。これが3回連続する確率は

\frac{5}{6} \times \frac{5}{6} \times \frac{5}{6}

で

\frac{125}{216}

です。

令和4年問93

A3判の紙の長辺を半分に折ると，A4判の大きさになり，短辺：長辺の比率は変わらない。A3判の長辺はA4判の長辺のおよそ何倍か。

ア	1.41
イ	1.5
ウ	1.73
エ	2

答え：ア
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学
解説：
A判やB判の紙のサイズは相似形になっており、縦横の比率は変わらず一つ上のサイズの半分になっています。

A4判の短辺を1、長辺をaとすると、A3の長辺は2、短辺はA4の長辺と同じaとなります。このとき、A4とA3の縦横比は同じなので、比例式を用いて

1:a=a:2

と表すことができます。比例式の内積と外積は等しいことから

a²=2

となり、a=√2 と求めることができます。これは約1.41に相当するため「ア」が正解です。

令和2年秋期問62

10進数155を2進数で表したものはどれか。

ア	10011011
イ	10110011
ウ	11001101
エ	11011001

答え：ア
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学

令和1年秋期問80

パスワードの解読方法の一つとして，全ての文字の組合せを試みる総当たり攻撃がある。“A”から“Z”の26種類の文字を使用できるパスワードにおいて，文字数を4文字から6文字に増やすと，総当たり攻撃でパスワードを解読するための最大の試行回数は何倍になるか。

ア	2
イ	24
ウ	52
エ	676

答え：エ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学

令和1年秋期問82

次の体系をもつ電話番号において，80億個の番号を創出したい。番号の最低限必要な桁数は幾つか。ここで，桁数には“020”を含むこととする。

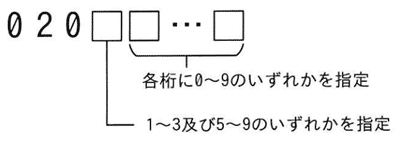
ア	11
イ	12
ウ	13
エ	14

答え：ウ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学

平成30年秋期問79

8ビットの2進データXと00001111について，ビットごとの論理積をとった結果はどれか。ここでデータの左方を上位，右方を下位とする。

ア	下位4ビットが全て0になり，Xの上位4ビットがそのまま残る。
イ	下位4ビットが全て1になり，Xの上位4ビットがそのまま残る。
ウ	上位4ビットが全て0になり，Xの下位4ビットがそのまま残る。
エ	上位4ビットが全て1になり，Xの下位4ビットがそのまま残る。

答え：ウ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学

平成30年春期問75

A～Zの26種類の文字を表現する文字コードに最小限必要なビット数は幾つか。

ア	4
イ	5
ウ	6
エ	7

答え：イ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学

平成29年秋期問98

次のベン図の網掛けした部分の検索条件はどれか。

ア	（not A） and （B and C）
イ	（not A） and （B or C）
ウ	（not A） or （B and C）
エ	（not A） or （B or C）

答え：イ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学

平成29年春期問72

二つの2進数 01011010 と 01101011 を加算して得られる2進数はどれか。ここで，2進数は値が正の8ビットで表現するものとする。

ア	00110001
イ	01111011
ウ	10000100
エ	11000101

答え：エ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学

平成28年秋期問91

2進数1011と2進数101を乗算した結果の2進数はどれか。

ア	1111
イ	10000
ウ	101111
エ	110111

答え：エ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学

平成27年春期問62

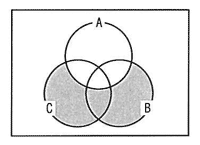
二つの集合AとBについて，常に成立する関係を記述したものはどれか。ここで，（X∩Y）は，XとYの両方に属する部分（積集合），（XUY）は，X又はYの少なくとも一方に属する部分（和集合）を表す。

ア	（AUB）は，（A∩B）でない集合の部分集合である。
イ	（AUB）は，Aの部分集合である。
ウ	（A∩B）は，（AUB）の部分集合である。
エ	（A∩B）は，Aでない集合の部分集合である。

答え：ウ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学

平成26年春期問51

パスワードの解読方法の一つとして，全ての文字の組合せを試みる総当たり攻撃がある。 “0”から“9”の10種類の文字を使用できるパスワードにおいて，桁数を4桁から6桁に増やすと，総当たり攻撃でパスワードを解読するための最大の試行回数は何倍になるか。

ア	1.5
イ	20
ウ	10
エ	1,024

答え：ウ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学

平成26年春期問57

図1のように二つの入力に対し，一つの出力を行うボックスがある。このボックスヘの入力は“賛成”か“反対”のいずれかであり，入力が二つとも“賛成”のときだけ“賛成”と出力し，その他のときは“反対”と出力する。図2のように，三つの入力を二つのボックスに入力したときの出力に関する記述のうち，正しいものはどれか。

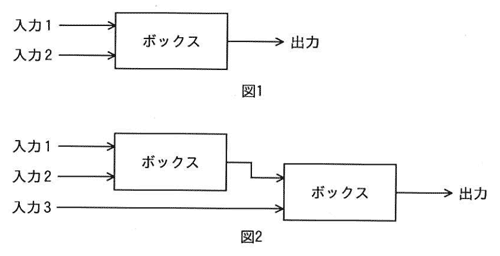
ア	入力が一つ以上“賛成”のときは常に，“賛成”と出力する。
イ	入力が二つ以上“賛成”のときは常に，“賛成”と出力する。
ウ	入力が二つ以上“反対”のときだけ，“反対”と出力する。
エ	入力が三つとも“賛成”のときだけ，“賛成”と出力する。

答え：エ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学

平成25年秋期問54

“男性のうち，20歳未満の人と65歳以上の人”に関する情報を検索するための検索式として，適切なものはどれか。

ア	男性 AND（20歳未満 AND 65歳以上）
イ	男性 AND（20歳未満 OR 65歳以上）
ウ	男性 OR（20歳未満AND 65歳以上）
エ	男性 OR（20歳未満 OR 65歳以上）

答え：イ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学

平成25年秋期問64

次の真理値表で示される入力x，yに対する出力zが得られる論理演算式はどれか。

x	y	z
0	0	1
0	1	0
1	0	0
1	1	0

ア	x AND y
イ	NOT（x AND y）
ウ	NOT（x OR y）
エ	x OR y

答え：ウ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学

平成25年秋期問76

2バイトで1文字を表すとき，何種類の文字まで表せるか。

ア	32,000
イ	32,768
ウ	64,000
エ	65,536

答え：エ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学

平成25年春期問82

排他的論理和を表す論理式はどれか。ここで，論理変数AとBに対する排他的論理和の真理値表は次のように表される。また，ANDは論理積，ORは論理和，NOTは否定を表す。

A	B	排他的論理和
0	0	0
0	1	1
1	0	1
1	1	0

ア	(A OR B) AND (A OR (NOT B))
イ	(A OR B) AND ((NOT A) OR (NOT B))
ウ	((NOT A) OR B) AND (A OR (NOT B))
エ	((NOT A) OR B) AND ((NOT A) OR (NOT B))

答え：イ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学

平成24年秋期問65

“商品値引き”表に示すとおり，値引き率が異なる商品群がある。30個買ったときに最も合計価格が安いのは，どのIDの商品か。ここで，値引き数量以上の個数を購入した場合に，合計価格に対して値引率で示す値引きが適用されるものとする。

商品値引き

商品ID	単価（円）	値引き数量（個）	値引率（％）
0001	30	30	30
0002	25	40	40
0003	40	20	50
0004	35	35	60

ア	0001
イ	0002
ウ	0003
エ	0004

答え：ウ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学

平成24年秋期問66

2進数に変換したとき，有限小数で表現できる10進数はどれか。

ア	0.1
イ	0.2
ウ	0.4
エ	0.5

答え：エ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学

平成24年秋期問72

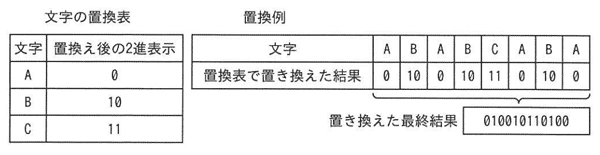
図に示すように，文字列の各文字を置換表に従って置き換える処理を考える。このような置換えを行った結果が“0110001010”であったとき，置換え前の文字列はどれか。

ア	ABBAAABB
イ	ACAAABB
ウ	ACABB
エ	CAAABB

答え：イ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学

平成24年秋期問79

16進数のA3は10進数で幾らか。

ア	103
イ	153
ウ	163
エ	179

答え：ウ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学

平成24年秋期問82

真理値表に対応する論理演算はどれか。

入力A	入力B	出力
0	0	0
0	1	0
1	0	0
1	1	1

ア	AND
イ	NOT
ウ	OR
エ	XOR

答え：ア
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学

平成24年春期問52

負の整数を2の補数で表現するとき，8桁の2進数で表現できる数値の範囲を10進数で表したものはどれか。

ア	-256～255
イ	-255～256
ウ	-128～127
エ	-127～128

答え：ウ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学

平成24年春期問69

札幌にある日本料理の店と函館にある日本料理の店をまとめて探したい。検索条件を表す論理式はどれか。

ア	（“札幌” AND “函館”） AND “日本料理”
イ	（“札幌” AND “函館”） OR “日本料理”
ウ	（“札幌” OR “函館”） AND “日本料理”
エ	（“札幌” OR “函館”） OR “日本料理”

答え：ウ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学

平成23年秋期問72

10進数の2，5，10，21を，五つの升目の白黒で次のように表す。

2 □□□■□
5 □□■□■
10 □■□■□
21 ■□■□■

　それぞれの升目が白のときは0，黒のときは升目の位置によってある決まった異なる正の値を意味する。この五つの升目の値を合計して10進数を表すものとすると，■■□□□が表す数値はどれか。

ア	12
イ	20
ウ	24
エ	30

答え：ウ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学

平成23年春期問56

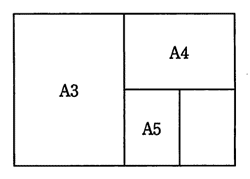
紙の大きさの規格は図のような相似形であり，例えばA判用紙では，A3の面積の半分がA4になるという関係にある。コピー機でA4サイズの原稿をA3サイズに拡大コピーするためには，どの拡大率（%）を選んだらよいか。ここで，拡大率は長い辺同士の比率を表す。

ア	122
イ	141
ウ	150
エ	200

答え：イ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学

平成22年秋期問68

任意の8ビットのデータXと，8ビットのデータ00001111をビットごとに排他的論理和をとった結果はどれか。ここで，各1ビットのデータAとデータBの排他的論理和をとった結果Cの値は次のように表される。また，データの左方を上位，右方を下位と呼ぶ。

排他的論理和

A	B	C
0	0	0
0	1	1
1	0	1
1	1	0

ア	Xの上位4ビットすべての0，1が反転し，下位4ビットはすべて1になる。
イ	Xの上位4ビットすべての0，1が反転し，下位4ビットはそのまま残る。
ウ	Xの上位4ビットはすべて0で，下位4ビットすべての0，1が反転する。
エ	Xの上位4ビットはそのままで，下位4ビットすべての0，1が反転する。

答え：エ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学

平成22年春期問52

2進数1.101を10進数で表現したものはどれか。

ア	1.2
イ	1.5
ウ	1.505
エ	1.625

答え：エ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学

平成22年春期問69

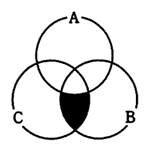
二つの集合AとBについて，常に成立する関係を記述したものはどれか。ここで，（X∩Y）は，XとYの共通部分（積集合），（X∪Y）は，X又はYの少なくとも一方に属する部分（和集合）を表す。

ア	（A∩B）は，Aでない集合の部分集合である。
イ	（A∩B）は，Aの部分集合である。
ウ	（A∪B）は，（A∩B）の部分集合である。
エ	（A∪B）は，Aの部分集合である。

答え：イ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学

平成21年秋期問64

8進数の55を16進数で表したものはどれか。

ア	2D
イ	2E
ウ	4D
エ	4E

答え：ア
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学

平成21年春期問64

2進数10110を3倍したものはどれか。

ア	111010
イ	111110
ウ	1000010
エ	10110000

答え：ウ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学

平成21年春期問71

次のベン図の黒色で塗りつぶした部分の検索条件はどれか。

ア	（not A） and B and C
イ	（not A） and （B or C）
ウ	（not A） or （B and C）
エ	（not A） or （B or C）

答え：ア
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学

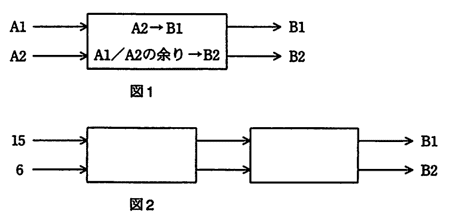
平成21年春期問72

図1のように二つの正の数値A1，A2を読み取り，二つの数値B1，B2を出力するボックスがある。B1にはA2と同じ数値を出力し，B2にはA1をA2で割った余りを出力する。図2のようにこのボックスを2個つないだ場合，A1=15，A2=6のとき後方のボックスのB1に出力される数値は幾らか。

ア	0
イ	3
ウ	6
エ	15

答え：イ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 離散数学