ITパスポート過去問集 - 応用数学

令和7年問63

データの尺度を名義尺度，順序尺度，間隔尺度，比例尺度の四つに分類したとき，間隔尺度に該当するものはどれか。

ア	学年
イ	血液型
ウ	時刻
エ	睡眠時間

答え：ウ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 応用数学

令和5年問77

受験者10,000人の4教科の試験結果は表のとおりであり，いずれの教科の得点分布も正規分布に従っていたとする。ある受験者の4教科の得点が全て71点であったときこの受験者が最も高い偏差値を得た教科はどれか。

単位　点

	平均点	標準偏差
国語	62	5
社会	55	9
数学	58	6
理科	60	7

ア	国語
イ	社会
ウ	数学
エ	理科

答え：ウ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 応用数学
解説：
偏差値は得点が集団内でどの程度の位置に相当するかを表す指標で、いわゆる学力偏差値の場合は集団の平均値が50、標準偏差が10になるように調整した値となります。このとき、偏差値は（得点－平均点）÷標準偏差×10＋50 という式で求められます。

問題の条件をこの式に当てはめると、国語の偏差値は（71－62）÷5×10＋50=68、同様に社会は67、数学は71、理科は65となり、数学の「ウ」が正解です。

令和4年問59

次のデータの平均値と中央値の組合せはどれか。

〔データ〕
10, 20, 20, 20, 40, 50, 100, 440, 2000

	平均値	中央値
ア	20	40
イ	40	20
ウ	300	20
エ	300	40

答え：エ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 応用数学
解説：
平均値はすべて足して個数で割ったもので、2700÷9=300です。中央値は小さい順または大きい順に並べたときに真ん中にある値で、40です。この2つを組み合わせた「エ」が正解です。

令和3年問66

RGBの各色の階調を，それぞれ3桁の2進数で表す場合，混色によって表すことができる色は何通りか。

ア	8
イ	24
ウ	256
エ	512

答え：エ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 応用数学
解説：
RGB方式は色の表現方法の一つで、「赤」（R：Red）、「緑」（G：Green）、「青」（B：Blue）の3色を様々な強度で組み合わせて色を表現します。

各色を3桁の2進数で表す場合、1色あたり2³=8段階の階調を表現することができます。これを3色組み合わせるので全体では8³=512色を表現することができます。「エ」が正解です。

令和1年秋期問72

3人の候補者の中から兼任も許す方法で委員長と書記を1名ずつ選ぶ場合，3人の中から委員長1名の選び方が3通りで，3人の中から書記1名の選び方が3通りであるので，委員長と書記の選び方は全部で9通りある。5人の候補者の中から兼任も許す方法で委員長と書記を1名ずつ選ぶ場合，選び方は何通りあるか。

ア	5
イ	10
ウ	20
エ	25

答え：エ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 応用数学

平成28年春期問98

それぞれが独立に点灯／消灯の操作ができる5個のランプが並んでいる。2個以上のランプが点灯しているパターンは何通りあるか。ここで，全てが点灯しているパターンは1通り，いずれか1個が点灯しているパターンは5通りと数えるものとする。

ア	4
イ	10
ウ	26
エ	32

答え：ウ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 応用数学

平成26年春期問63

a，b，c，d，e，fの6文字を任意の順で1列に並べたとき，aとbが隣同士になる場合は，何通りか。

ア	120
イ	240
ウ	720
エ	1,440

答え：イ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 応用数学

平成22年秋期問72

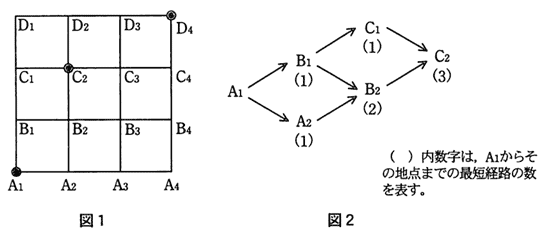
図1のA₁地点からC₂地点へ行くとき，通過する地点が最も少なくてすむ最短経路は，図2のように数えることによって3通りあることが分かる。A₁地点から，C₂地点を経由して，D₄地点へ行く最短経路は何通りあるか。

ア	6
イ	9
ウ	12
エ	20

答え：イ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 応用数学

平成22年秋期問82

a，b，c，d，e，fの6文字すべてを任意の順で一列に並べたとき，aとbが両端になる場合は，何通りか。

ア	24
イ	30
ウ	48
エ	360

答え：ウ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 応用数学

平成22年春期問67

表のA列とB列に0から9までの数字のすべての組合せが入っており，全部で100行ある。表からA列の値がB列の値以下である行をすべて取り除く。残りは何行あるか。

A	B
0	0
0	1
0	2
︙	︙
9	8
9	9

ア	40
イ	45
ウ	50
エ	55

答え：イ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 応用数学

平成21年秋期問70

0から1までの一様乱数からXとYを取り出すことを600回繰り返す。このときY＜Xを満たす回数の期待値は幾らか。

ア	150
イ	200
ウ	300
エ	400

答え：ウ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 応用数学

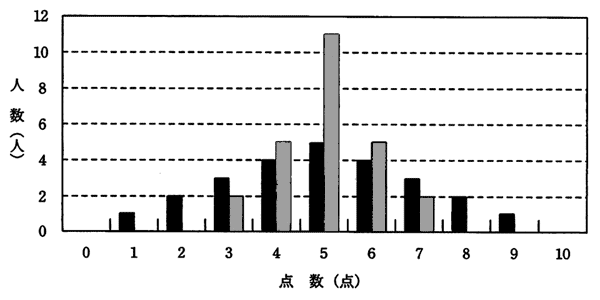
平成21年春期問80

横軸を点数（0～10点）とし，縦軸を人数とする度数分布のグラフが，次の黒い棒グラフになった場合と，グレーの棒グラフになった場合を考える。二つの棒グラフを比較して言えることはどれか。

ア	分散はグレーの棒グラフが，黒の棒グラフより大きい。
イ	分散はグレーの棒グラフが，黒の棒グラフより小さい。
ウ	分散はグレーの棒グラフと，黒の棒グラフで等しい。
エ	分散はこのグラフだけで比較することはできない。

答え：イ
分野：テクノロジ系 › 基礎理論 › 基礎理論 › 応用数学